filmov
tv
Proof: Vertices of Strong Tournament Lie on Triangles | Graph Theory

Показать описание
We prove that every vertex of a strongly connected tournament graph lie on a triangle (a 3-cycle). #GraphTheory
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
Proof: Vertices of Strong Tournament Lie on Triangles | Graph Theory
Proof: Every Tournament has Hamiltonian Path | Graph Theory
Proof for Distances from Tournament's Maximum Outdegree Vertex | Graph Theory
Intro to Tournament Graphs | Graph Theory
Proof: Tournament is Transitive iff it has No Cycles | Graph Theory
(4E) Graph Theory and Strong Induction
Graph Theory - Tournaments (Lecture 17)
Tournament graph
V6GTU4S60 Results on tournaments
Probabilistic Methods - 1.2 Graph Theory - Part 1 - Tournament
Math 432: Graph Theory - Directed Graphs (3 of 3)
Math's Map Coloring Problem - The First Proof Solved By A Computer
Hamilton Tournaments - 20
Proof: Ore's Theorem for Hamiltonian Graphs | Sufficient Condition for Hamilton Graphs, Graph T...
mod04lec18 - Chromatic Coding for Feedback Arc Set on Tournaments
Proof: Every Graph Contains Minimum Degree Length Path | Graph Theory
α perfection of interval graphs,chordal graphs, expansion lemma proof for weak perfect conjecture
Induction With Graphs Example 3.2
SiGMa 2017 Maria Chudnovsky, Coloring graphs with forbidden induced subgraphs
An Efficient Semi-Streaming PTAS for Tournament Feedback Arc Set with Few Passes
Covering and Packing: Erdos Posa for Feedback Arc Set in Tournaments
Graph Theory - Tournament
5.9 Tournament
Digraphs 5 - Hamiltonian
Комментарии
 0:07:32
0:07:32
 0:07:59
0:07:59
 0:08:37
0:08:37
 0:09:53
0:09:53
 0:10:40
0:10:40
 0:47:32
0:47:32
 0:48:02
0:48:02
 0:01:21
0:01:21
 0:21:55
0:21:55
 0:05:51
0:05:51
 0:12:09
0:12:09
 0:09:04
0:09:04
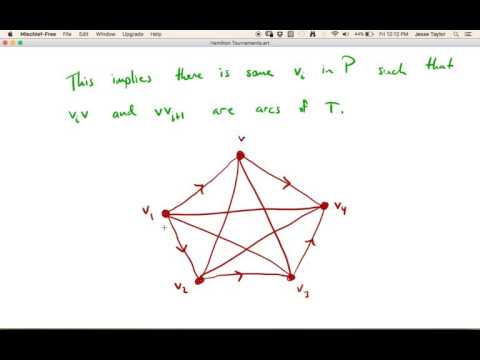 0:11:17
0:11:17
 0:14:36
0:14:36
 0:46:13
0:46:13
 0:05:22
0:05:22
 1:08:43
1:08:43
 0:02:38
0:02:38
 0:54:42
0:54:42
 0:19:03
0:19:03
 1:46:54
1:46:54
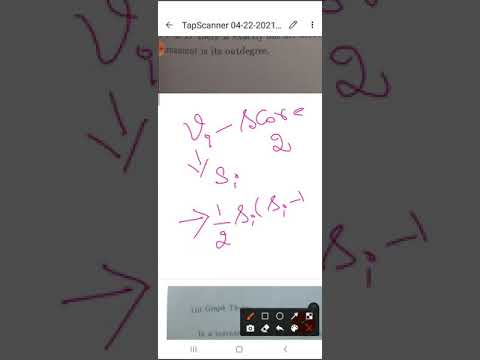 0:20:09
0:20:09
 0:02:54
0:02:54
 0:30:39
0:30:39