Bubble sort algorithm

See complete series on sorting algorithms here:
This series is in progress, we will be adding lessons into this series every week.
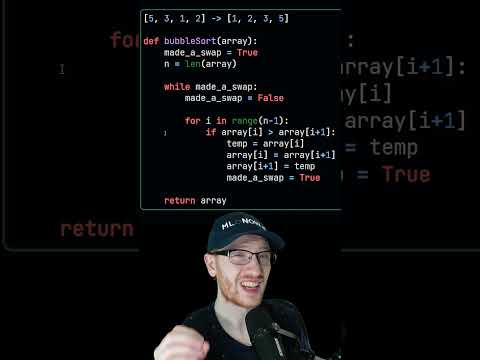
In this lesson, we have described Bubble sort algorithm and analyzed its time complexity.
Series on Time Complexity:

Subscribe to our channel to get updates on new lessons.

You may also like us on Facebook:

[FRSS]

Finally, a tutorial explaining not only the logic of the algorithm, but the logic behind it's iteration. Thanks a bunch!

[blueskyrelaxmusic]

This is what we need in youtube. Great lecture with great timing.Good job.

[ibzih]

Dude this 10 mins video is worth my uni's multiple hour lectures. Very helpful! Thanks!

[mycodeschool]

Hi Ravi,
I guess you are talking about 6:03. Outer loop is running from 1 to n-1 (we could have run from 0 till n-2 also) which is n-1 times. If you bubble up n-1 elements, last one - nth one will automatically be in place. So, no need to run n time. Inner loop is running from 0 till n-2. It's again n-1 times. So, it looks correct to me.

[curiouswithAi]

This channel is a true Gem For Students. Got an exam tomorrow. Would have been really difficult without You. Thank You so much for

[allblue]

i swear this is way better than some of the professors video in schools

[minimalist_pc]

your explanation is perfectly clear and the coding is really simple. Thank you so much!

[saltyfish]

You are the best explainer I have ever seen

[preetshah]

This is the best channel for learning algorithm and data structure. I am coming back here after 5 years

[cagnusmarlsen]

In all of the videos the voice and the language is pretty clear and sharp so there's no need for sub-titles.

[mauriceudoh]

This is simplified enough for a comprehension, Thanks

[ahinsa__parmo__dharam]

When you reach for O(n), i'm shocked because I had never seen this version of bubble sort .. hatsoff to you.

[viditsinghbrahmania]

I can not even fathom how much effort would be needed to make something like this, and it is freely available!
I don't know if any of you have noticed, but he is using MS Paint. And I didn't know it could ever be used to make something useful, let alone this.

I always used to undermine myself, considering that I am not a 'programmer'(never really understood these simple concepts, due to shitty teachers), but in the last few weeks, I've learnt so much only because of you and other good content on the internet. And now I proudly say I enjoy programming and I am a programmer!

[chelseakatsidzira]

very helpful thank you so much. this is honestly the most clear cut explanation on youtube

[ANILKHANDEI]

The video is perfect. Thanks for the ultimate collection. One check is that outer loop runs n-1 times and inner loop is an arithmetic progression n*(n-1)/2 instead of n-1. The total being n+ (n*(n-1)/2= O(n^2). Just wanted to point out. Let me know if my consideration is wrong.

[manishasharma-hymj]

Thank you so much for the series of sorting algorithms.
I request you to give explanation on heap sort.

[sriharshasaraswathula]

The outer loop must execute from 0 t0 n-1, otherwise last element will not be sorted.
code:
for(int k=0;k<n-1;k++){
int flag=0;
for(int i=0;i<n-k-1;i++){
if(A[i] > A[i+1]){
flag=1;
int temp = A[i];
A[i] = A[i+1];
A[i+1] = temp;
}
}
if(flag == 0){
break;
}
}

[shreyasinghthakur]

For people wondering why n-2 and not n-1
Explaination - In an array, "n" typically represents the total number of elements in the array. So, "n-1" would refer to the index of the last element in the array since array indexing usually starts from 0.

For example, let's say we have an array with 5 elements. "n" would be 5, and "n-1" would be 4, representing the index of the last element in the array. So if we have an array called `arr`, `arr[4]` would be the last element.

[maheshvalikar]

You are the best presenter i have ever seen. Very much useful. This kind of tutorials what we expect. Great job bro.

[goldenotis]

Best big o notation explanation I've seen so far and its not even a big o analysis video