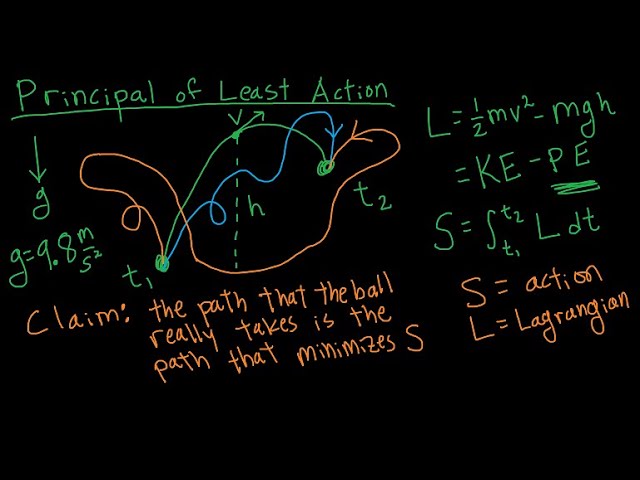
The Principle of Least Action

[High School Level] In this video I explain the principle of least action, and show that it is equivalent to the regular way of doing things.

[bankaikun]

I'm confused at the particular step demonstrated at 20:53. The first order approximation uses the derivative evaluated at the x(t)+EN(t). Why isn't it just x(t)? I thought the expansion was around x(t), so the derivative should be evaluated at just x(t).

For instance, you wrote above that, f(x+E)=f(x)+Ef'(x)+....
Here f' is evaluated at x, rather than x+E. Also what is f' wrt? Is it df/dx? Or df/d(x+E)?

I'm following the formula, f(x)=f(a)+(df(a)/dx)(x-a)+... where in the former case, x=x(t)+EN(t), and a=x(t). As for the latter case, x=x+E and a=x.

[thiscommentsdeleted]

This is so underrated. Great job, Noah!

[jacoboribilik]

17:25 the rastafari equation. Thank you for taking the time to make this video.

[knarfamoranemix]

@ Michał Prządka :
The Taylor expansion seems correct to me.
First a comment on the equation from Noah's comment : In f(x + E) = f(x) + E*f'(x)+.., the ' can mean deriving by x or by E, which amounts to the same thing I think.
Define g(eps) = S(x + eps*eta)
Hence g(0) = S(x)
To find the value of g(eps), we can use the Taylor expansion ('meaning deriving by eps) :
g(0+eps) = g(0) + eps*g'(0) = S(x) + eps*S'(x)
= S(x) + eps*(S'(x+eps*eta) at eps=0)

That said, I have many issues with the derivation.

I have a question too :
That principle of least action looks false. It is easly to find unrealistic paths that have a lower action than the real path. For example, in a gravitational field, have a particle follow a higher path at slower speed. Hence the kinetic energy will be lower, the potential energy higher and the travel time longer.

In order to meaningfully talk about a minimum, one must consider a set of paths, all of which violate the laws of physics, except for the real one. In what way may the laws of physics be varied to form that set ?

[cui_]

now finally i have video of Feynman lecture too !!!
nicee

[tehnik]

What if the bracketed part in 51:55 (claimed to be 0) were a trigonometric function which has the same function values at t1 and t2, divided by eta(t). Wouldn't that also leave the integral to be 0?
On what grounds could we reject this?

[NancyMancarious]

Wow! I never really understood why the integration by parts is done so. We used to memorize this as students!

[ositchukwu]

39:07 there should be eta dot not just eta. Great video thank you.

[TheLogvasStudio]

1) I prefer to explain the same stuff in different order, because then math is much more simpler.

2) Imagine, we are creating kinematics from scratch.

2.1) We have some stable processes, that we could use, to measure time.

2.2) We able to measure distance between objects with a ruler. Sometimes, we even can create a blockade on a known distance, in order to measure, how much time[phases of stable process] would it take for object to reach the blockade.

2.3) We also are able to measure resulting force, that object experience, using spring deformation.

3.1) When we do the measurements, it is really a bunch of points of measured force/time/location combinations.

3.2) But from those points, we could model a trajectory path of a body.

3.3) Based on measurements, we could come up with an equation of motions, that would explain it and our trajectory.

3.4) In Newtonian mechanics, we use forces, that produce acceleration, as a useful modelling concepts, not going for 3+ derivatives.

4) Let us set up some definitions:

4.1) v=d/t or d=vt
4.2) v=(vf+vi)/2
average speed in linear acceleration case
4.3) t=(vf-vi)/a
4.4) F=ma
4.5) E=F*d=ma*d=mgh

5.1) Put v from 4.2 into 4.1: d=(vf+vi)/2*t
5.2) Put t from 4.3 into 5.1: d=(vf+vi)/2*(vf-vi)/a
d=(vf²-vi²)/2a
5.3) From 4.5: E=ma*(vf²-vi²)/2a
E=m(vf²-vi²)/2

6.1) So way we derive KE and PE equations from Newtons law.
6.2) All accelerations, that we use in our model, are linear, therefore we know, that between 2 points in trajectory there wouldn't be any spooky pikes. Principle of stationary action is just a conquence of us using forces in order to describe all motion.