filmov
tv
8.3 - Identification in Linear Setting

Показать описание
In this part of the Introduction to Causal Inference course, we show that instrumental variables allow us to identify the ATE if we make a linearity assumption. Please post questions in the YouTube comments section.
How to Distinguish Between Linear & Nonlinear : Math Teacher Tips
Linear Programming (Optimization) 2 Examples Minimize & Maximize
Learning to Identify Linear Pairs of Angles
Linear Equations - Algebra
Learn how to identify the slope and y intercept from a linear equation in slope intercept
Linear Functions
Linear Equation | Solving Linear Equations
Difference Between Linear and non Linear Equation s.
Linear Transformation in Self Attention | Transformers in Deep Learning | Part 3
Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts
Determining if equations are linear - Free Math Videos - Online Tutor
Solving Linear Equation in One Variable #math #mathematics #equation #linearequations #mathtricks
How To Find The Slope and Y Intercept of a Line | Linear Equations - Algebra
Difference between linear and nonlinear Differential Equation|Linear verses nonlinear DE
How to Find the Matrix of a Linear Transformation
What is a linear pair
How to check Linear and Non Linear Differential Equation EASY TECHNIQUE | Linear non linear DE
How to draw graph of the Linear Equation y=2x+3 #math #tutor #mathtrick #learning #shorts #graph
How to determine the domain of a linear function
Graphs of linear equations | Linear equations and functions | 8th grade | Khan Academy
Writing A Linear Equation From A Function Table
Number of solutions to linear equations | Linear equations | Algebra I | Khan Academy
How to write a linear equation in standard form
Linear, Quadratic, and Exponential Models
Комментарии
 0:01:57
0:01:57
 0:15:08
0:15:08
 0:02:15
0:02:15
 0:32:05
0:32:05
 0:01:06
0:01:06
 0:15:01
0:15:01
 0:11:20
0:11:20
 0:04:56
0:04:56
 0:29:37
0:29:37
 0:06:52
0:06:52
 0:02:39
0:02:39
 0:00:57
0:00:57
 0:15:16
0:15:16
 0:03:29
0:03:29
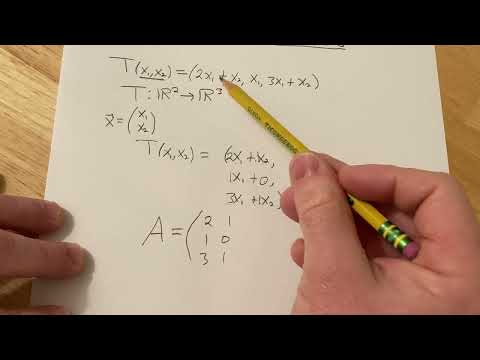 0:05:19
0:05:19
 0:03:43
0:03:43
 0:07:50
0:07:50
 0:00:46
0:00:46
 0:02:42
0:02:42
 0:13:10
0:13:10
 0:08:40
0:08:40
 0:05:27
0:05:27
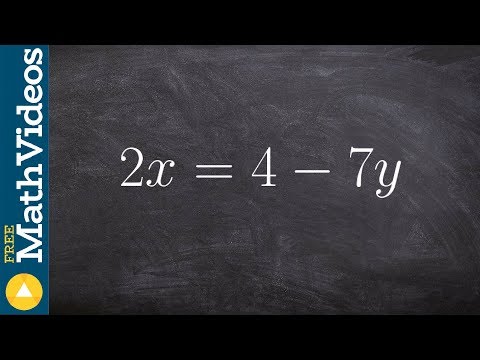 0:02:19
0:02:19
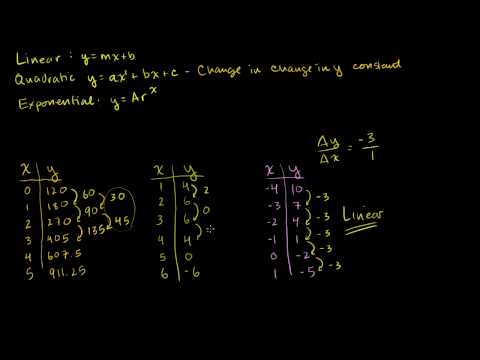 0:08:15
0:08:15