filmov
tv
Applications of triple integrals, Multivariable Calculus Unit 4 Lecture 6

Показать описание
We look at three applications for integrating functions of the form w=f(x,y,z) over regions in the (x,y,z)-plane: (1) volume computations, (2) average value computations, and (3) center of mass computations. This is Multivariable Calculus Unit 4 Lecture 6.
We begin by connecting the concept of triple integrals to the volume computations similar to area computations in double integrals. If we have a closed bounded region 𝐷 in 𝑥𝑦𝑧-space that can be described with inequalities, we can set up the triple integral of one over 𝐷 to compute its volume. We denote 𝑑𝑉 as the differential volume element, which is a shorthand for 𝑑𝑥𝑑𝑦𝑑𝑧, or any permutation of these differentials depending on the region type.
Volume of 𝐷=∭_𝐷 1 𝑑𝑉
We then discuss how to compute the average value of a scalar-valued function 𝑓 of three variables over a domain 𝐷. The average value is the triple integral of 𝑓 over 𝐷 divided by the volume of 𝐷. This can be re-written as a ratio of integrals:
Average value of 𝑓 = ∭_𝐷 𝑓(𝑥,𝑦,𝑧) 𝑑𝑉 /∭_𝐷 1 𝑑𝑉.
The final application we cover is computing the center of mass for a non-uniform three-dimensional object. The center of mass is the point (X,Y,Z) where we can balance the object. We find it by dividing the moments by the total mass 𝑀:
(X,Y,Z) = (𝑀𝑦𝑧/𝑀, 𝑀𝑥𝑧/𝑀, 𝑀𝑥𝑦/𝑀).
#calculus #multivariablecalculus #mathematics #tripleintegral #integration #iitjammathematics #calculus3 #averagevalue #centerofmass
We begin by connecting the concept of triple integrals to the volume computations similar to area computations in double integrals. If we have a closed bounded region 𝐷 in 𝑥𝑦𝑧-space that can be described with inequalities, we can set up the triple integral of one over 𝐷 to compute its volume. We denote 𝑑𝑉 as the differential volume element, which is a shorthand for 𝑑𝑥𝑑𝑦𝑑𝑧, or any permutation of these differentials depending on the region type.
Volume of 𝐷=∭_𝐷 1 𝑑𝑉
We then discuss how to compute the average value of a scalar-valued function 𝑓 of three variables over a domain 𝐷. The average value is the triple integral of 𝑓 over 𝐷 divided by the volume of 𝐷. This can be re-written as a ratio of integrals:
Average value of 𝑓 = ∭_𝐷 𝑓(𝑥,𝑦,𝑧) 𝑑𝑉 /∭_𝐷 1 𝑑𝑉.
The final application we cover is computing the center of mass for a non-uniform three-dimensional object. The center of mass is the point (X,Y,Z) where we can balance the object. We find it by dividing the moments by the total mass 𝑀:
(X,Y,Z) = (𝑀𝑦𝑧/𝑀, 𝑀𝑥𝑧/𝑀, 𝑀𝑥𝑦/𝑀).
#calculus #multivariablecalculus #mathematics #tripleintegral #integration #iitjammathematics #calculus3 #averagevalue #centerofmass
Комментарии
 0:16:27
0:16:27
 0:17:22
0:17:22
 0:06:30
0:06:30
 0:10:06
0:10:06
 0:07:13
0:07:13
 0:15:29
0:15:29
 1:06:32
1:06:32
 0:09:14
0:09:14
 0:09:48
0:09:48
 0:20:34
0:20:34
 3:33:32
3:33:32
 0:03:41
0:03:41
 0:02:01
0:02:01
 3:20:10
3:20:10
 1:47:22
1:47:22
 0:05:59
0:05:59
 0:25:40
0:25:40
 0:08:10
0:08:10
 0:12:16
0:12:16
 0:10:43
0:10:43
 1:34:24
1:34:24
 0:20:45
0:20:45
 0:14:54
0:14:54
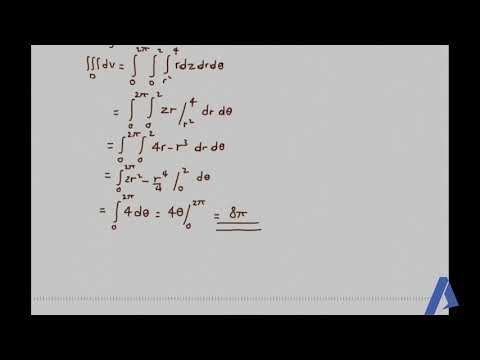 0:06:05
0:06:05