filmov
tv
Linear Algebra: Singular Value Decomposition (Full lecture)
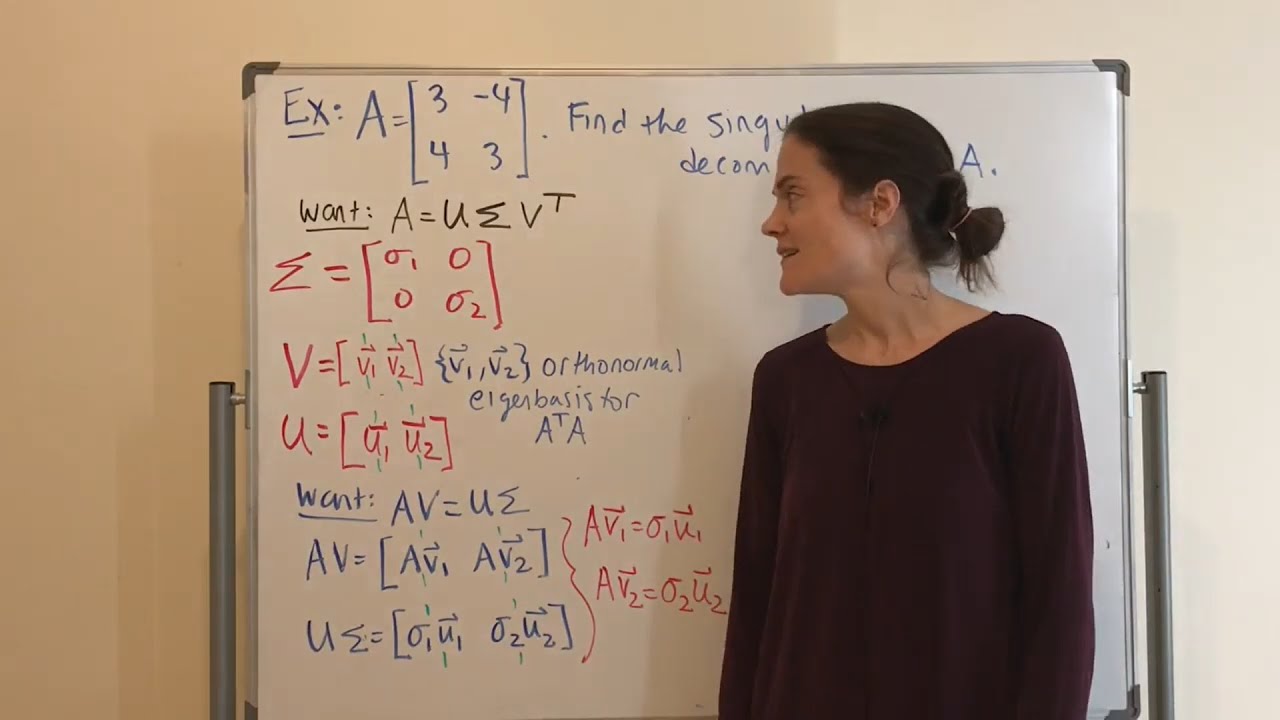
Показать описание
Singular Value Decomposition (the SVD)
Determine the Singular Value Decomposition of a Matrix
SVD Visualized, Singular Value Decomposition explained | SEE Matrix , Chapter 3 #SoME2
Singular Value Decomposition (SVD): Overview
What is the Singular Value Decomposition?
Singular Value Decomposition (SVD) Problem | Full Explanation
Linear Algebra: Singular Value Decomposition (Full lecture)
An example of a singular value decomposition
Gilbert Strang: Singular Value Decomposition
How to calculate the singular values of a matrix
Singular Value Decomposition: 2x2 Concrete Example | Linear Algebra | Ingenium Academy
Linear Algebra Example: The Singular Value Decomposition
6. Singular Value Decomposition (SVD)
Linear Algebra - Lecture 42 - The Singular Value Decomposition
Singular Value Decomposition | Linear algebra episode 9
Singular value decomposition with example #svd #singularvalue #decomposition #linearalgebra
Linear Algebra 23f: Introducing the Celebrated Singular Value Decomposition (SVD)
Singular Value Decomposition (SVD): Mathematical Overview
Computing the Singular Value Decomposition
7.4 - The Singular Value Decomposition.mp4
Lecture: The Singular Value Decomposition (SVD)
Singular Values vs. Eigenvalues : Data Science Basics
SINGULAR VALUE DECOMPOSITION (SVD) /VTU/ECE/4THSEM/ES&LA
Linear Algebra 9.5 Data Compression Using Singular Value Decomposition
Комментарии
 0:14:11
0:14:11
 0:11:00
0:11:00
 0:16:28
0:16:28
 0:06:44
0:06:44
 0:07:40
0:07:40
 0:11:27
0:11:27
 0:54:01
0:54:01
 0:06:14
0:06:14
 0:05:06
0:05:06
 0:03:20
0:03:20
 0:09:16
0:09:16
 0:10:40
0:10:40
 0:53:34
0:53:34
 0:17:35
0:17:35
 0:31:17
0:31:17
 0:14:08
0:14:08
 0:12:01
0:12:01
 0:12:51
0:12:51
 0:11:36
0:11:36
 0:38:31
0:38:31
 0:44:36
0:44:36
 0:04:45
0:04:45
 0:14:05
0:14:05
 0:10:00
0:10:00