filmov
tv
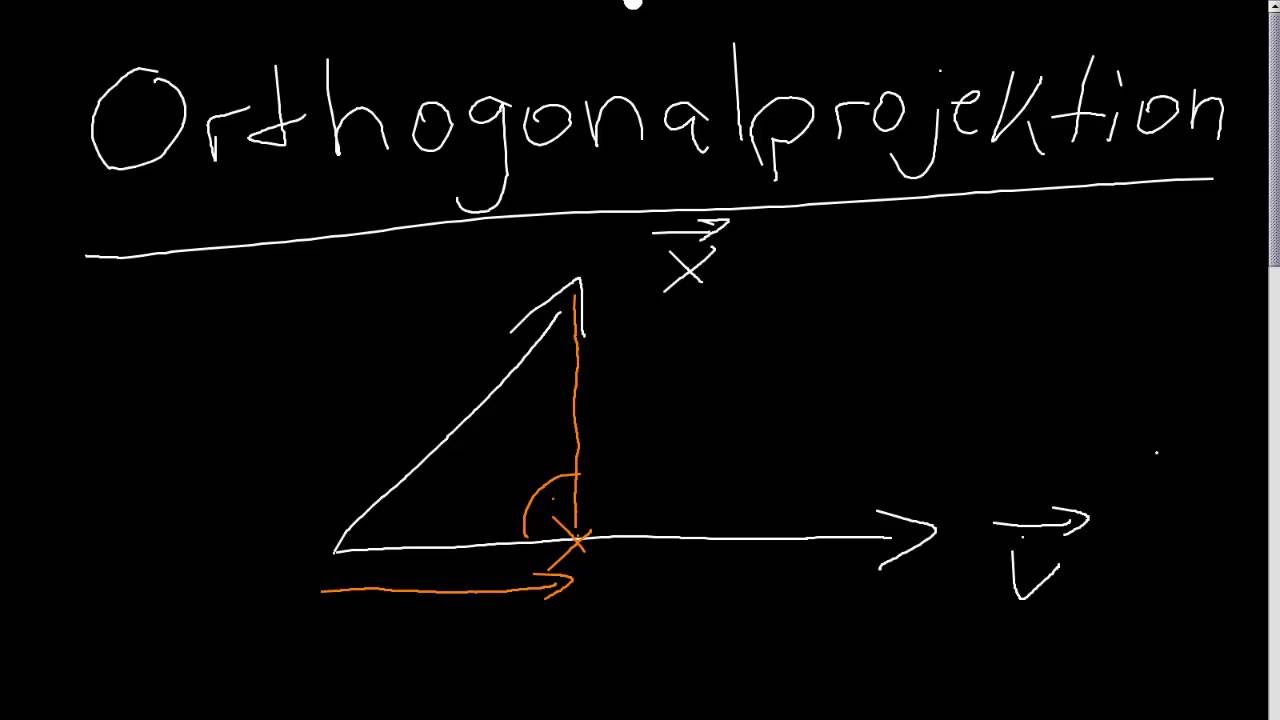
[Lineare Algebra und Geometrie] Berechnung der Orthogonalprojektion eines Vektors
Показать описание
Was ist eine Orthogonalprojektion und wie können wir sie für einen gegebenen Vektor berechnen?
0:06:58
Lineare Algebra | Denkanstoß zu Vektoren, Matrizen, Linearkombinationen | Mathe by Daniel Jung
0:07:00
[Lineare Algebra und Geometrie] Berechnung der Orthogonalprojektion eines Vektors
0:19:39
Grundlagen VEKTOREN – Einstieg Vektorgeometrie einfach erklärt
0:08:47
Grundlagen Vektoren (Analytische Geometrie)
0:05:22
Rechteck - Flächeninhalt und Umfang berechnen | Mathematik - ganz einfach erklärt! | Lehrerschmidt
0:11:19
Mathe ABITUR Aufgabe – Geraden und Ebenen (Analytische Geometrie, Vektoren)
0:03:38
Abbilden in eine Koordinatenebenebene, senkrechte Projektion, Matrizen, Mathe by Daniel Jung
0:05:54
Drehmatrix, Lineare Abbildungen, Herleitung, Lineare Algebra, Mathe by Daniel Jung
0:05:52
Lotfußpunktverfahren, Abstand Punkt Gerade, Vektorgeometrie | Mathe by Daniel Jung
0:06:27
Lineare Abbildung und Affine Abbildung, Übersicht, Lineare Algebra, Mathe by Daniel Jung
0:11:08
|Lineare Algebra und Geometrie] Rückwärtssubstitution
0:02:11
3 Vektoren auf Komplanarität untersuchen, Komplanar, linear abhängig, unabhängig
0:59:27
Was ist lineare Algebra? Und wofür braucht man Vektorräume?
0:11:42
VEKTOREN linear abhängig und unabhängig prüfen – lineare Abhängigkeit Vektoren
0:04:10
Spurpunkte von Geraden mit den Koordinatenebenen, Vektorgeometrie | Mathe by Daniel Jung
0:17:02
MÜNDLICHES ABITUR Mathe Vektoren – Komplette Mündliche Prüfung, Abiturprüfung Zusammenfassung
0:00:51
Abstand zweier Punkte in der Ebene berechnen | Abstandsformel für Punkte | Lineare Algebra
0:08:55
Würfel zeichnen und fehlende Koordinaten bestimmen | 3D, Vektorrechnung, Abitur
0:00:40
Spurpunkte von Geraden im Raum | das hast du noch nicht gesehen! Beispiel | Lineare Algebra
0:04:31
Flugzeugaufgabe, Vektoren, Geraden, Analytische Geometrie | Mathe by Daniel Jung
2:49:29
Livestream zu Lineare Algebra: Altklausur Teil 1, Duisburg/Essen
0:09:17
Schattenpunkt berechnen Vektoren – Schattenwurf Aufgabe
0:46:43
🚀🚀🚀 ZUSAMMENFASSUNG ABI 2025 VEKTOREN | Diese 9 Aufgaben kommen immer im Mathe Abitur dran!
0:11:36
[Lineare Algebra und Geometrie] Die darstellende Matrix einer linearen Abbildung
Комментарии