filmov
tv
Knapsack 0/1 problem by dynamic Programming in Hindi

Показать описание
Dynamic programming is based on the principle of optimality (also coined by Bellman). The principle of optimality states that no matter whatever the initial state and initial decision are, the remaining decision sequence must constitute an optimal decision sequence with regard to the state resulting from the first decision. The principle implies that an optimal decision sequence is comprised of optimal decision subsequence.
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays val[0..n-1] and wt[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item, or do’t pick it (0-1 property).
Algorithm:
Dynamic-0-1-knapsack (v, w, n, W) for w = 0 to W do c[0, w] = 0 for i = 1 to n do c[i, 0] = 0
for w = 1 to W do if i ≤ the if vi + c[i-1, w-wi] then c[i, w] = vi + c[i-1, w-wi] else c[i, w] = c[i-1, w] else c[i, w] = c[i-1, w]
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays val[0..n-1] and wt[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item, or do’t pick it (0-1 property).
Algorithm:
Dynamic-0-1-knapsack (v, w, n, W) for w = 0 to W do c[0, w] = 0 for i = 1 to n do c[i, 0] = 0
for w = 1 to W do if i ≤ the if vi + c[i-1, w-wi] then c[i, w] = vi + c[i-1, w-wi] else c[i, w] = c[i-1, w] else c[i, w] = c[i-1, w]
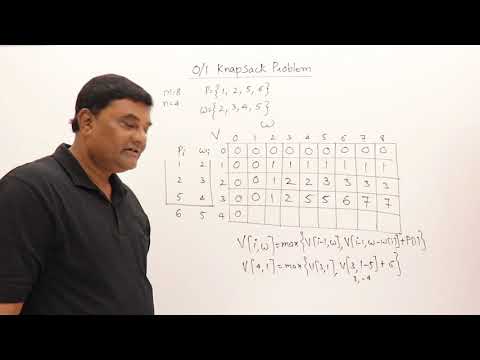 0:28:24
0:28:24
 0:13:29
0:13:29
 0:15:50
0:15:50
 0:17:00
0:17:00
 0:21:41
0:21:41
 0:16:40
0:16:40
 0:46:18
0:46:18
 0:20:30
0:20:30
 0:19:11
0:19:11
 0:09:06
0:09:06
 0:17:04
0:17:04
 0:08:11
0:08:11
 0:22:12
0:22:12
 0:16:56
0:16:56
 0:00:57
0:00:57
 0:19:04
0:19:04
 0:25:45
0:25:45
 0:11:08
0:11:08
 0:14:42
0:14:42
 0:00:08
0:00:08
 0:08:21
0:08:21
 0:37:33
0:37:33
 0:10:54
0:10:54
 0:15:45
0:15:45