filmov
tv
The 0/1 Knapsack Problem (Demystifying Dynamic Programming)

Показать описание
📹 Intuitive Video Explanations
🏃 Run Code As You Learn
💾 Save Progress
❓New Unseen Questions
🔎 Get All Solutions
I was inspired to do this video after seeing that Tuschar Roy had covered this problem. He did a good job, but I feel it very necessary to stress what is really happening and what each cell REALLY means.
Dynamic programming is about subproblems, not remembering patterns to fill cells in with. I watched EVERY ONE of Tuschar Roy's videos and found myself MEMORIZING how to fill out the cells INSTEAD of really knowing what was going on.
I hope this video sheds light on what this problem is really trying to express.
You can also do it TOP DOWN with recursion where we investigate all expressions of the subproblems to find the optimal solution. The book Elements of Programming Interviews by Aziz Adnan has a very good version of this. The problem is 17.6 in that book.
++++++++++++++++++++++++++++++++++++++++++++++++++
Question: Write a program for the knapsack problem that selects a subset of items that has maximum value and satisfies the weight constraint. All items have integer weights and values. Return the value of the subset.
Can we do it greedily?
0/1 means you cannot split an item. If you could split an item, you could solve this greedily by sorting the item entries by value and then picking from greatest value to least. When you run out of space in your "sack", you'd split the last item and then you would have maximized weight vs value.
Brute Force: We could consider all subsets of items in a complete search and take on the cost of exponential time of 2^n (we will explain this in another video).
Greedy doesn't work, brute forcing won't make the cut, now what? What can we do now?
Dynamic Programming.
Notice that we can subproblem this.
Dynamic programming is not about stupid magic tables that you see people fill out, it is not about guessing. DP is about remembering the solutions to subproblems so that we can find the globally optimal solution. We just subproblemed this recursively.
This is where the table comes from. Each cell MEANS SOMETHING.
IT IS THE ANSWER TO THE QUESTION.
If we solve all the subproblems and remember all answers then we will find the globally optimal answer.
The subproblems are represented by what is called a recurrence equation.
Complexities
n = total items
m = max weight (max weight constraint)
Time: O(nm) (we will be solving this many subproblems)
Space: O(nm) (we will store the results of n*m subproblems)
++++++++++++++++++++++++++++++++++++++++++++++++++
++++++++++++++++++++++++++++++++++++++++++++
The 0/1 Knapsack problem is question 17.6 in the fantastic book Elements of Programming Interviews.
Комментарии
 0:20:30
0:20:30
 0:13:29
0:13:29
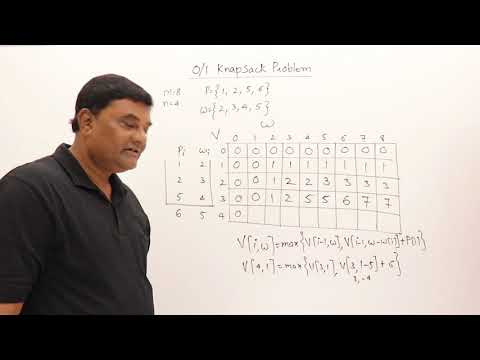 0:28:24
0:28:24
 0:09:06
0:09:06
 0:46:18
0:46:18
 0:15:50
0:15:50
 0:18:51
0:18:51
 0:30:52
0:30:52
 0:01:00
0:01:00
 0:41:19
0:41:19
 0:17:00
0:17:00
 0:18:07
0:18:07
 0:35:21
0:35:21
 0:10:54
0:10:54
 0:19:11
0:19:11
 0:05:16
0:05:16
 0:18:41
0:18:41
 0:28:13
0:28:13
 0:00:36
0:00:36
 0:14:09
0:14:09
 0:12:00
0:12:00
 0:01:27
0:01:27
 0:10:29
0:10:29
 0:16:56
0:16:56