Curve Fitting for Understanding Michael Levitt 14May2020

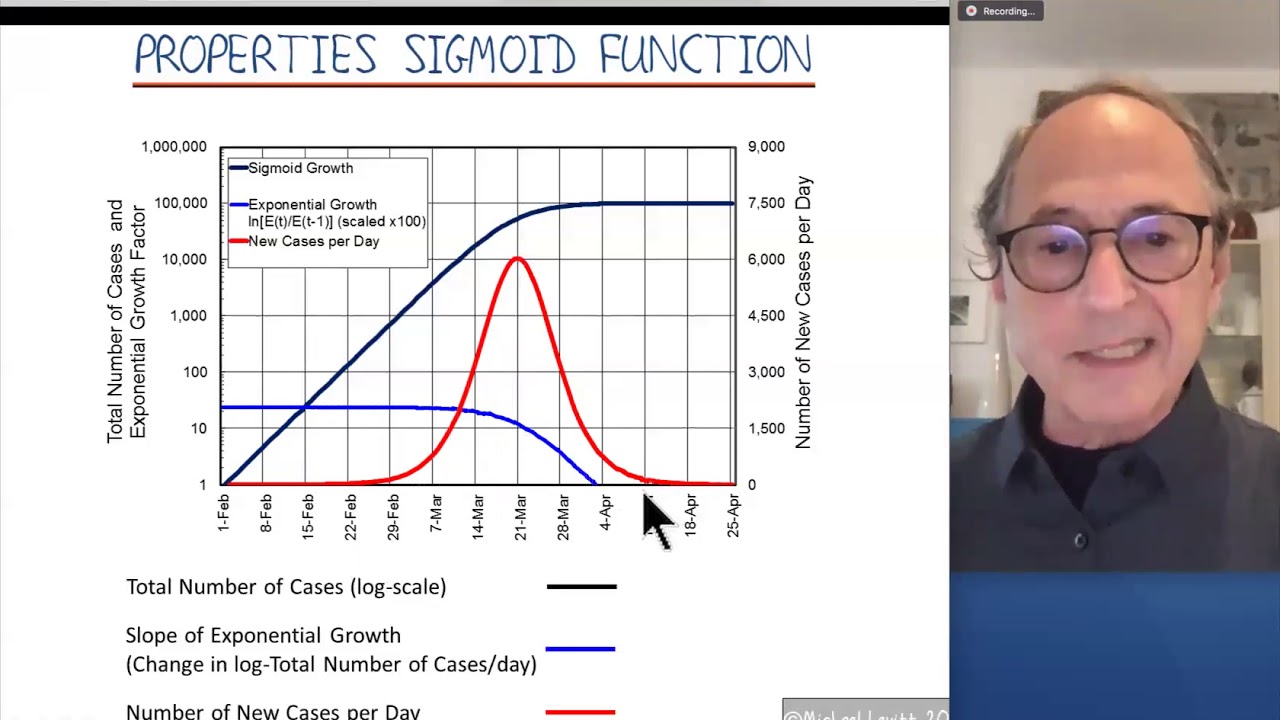
This is Part 2. Fitting viral growth data with simple mathematical functions can give important insights into how epidemics will grow. Here we illustrate two commonly used growth curves, the Sigmoid Function and the Gompertz Function. While superficially similar, they are really very different.

[sarasandegren]

I just want to thank you for standing up for your calculations of covid 19. As a Swed and economist I have followed your videos on Youtube with great interest.

[chasekard]

Great Michael. Keep going. Will show it to my grandchildren who look blankly when I say they need to know maths for future success.

[vicmartinez]

The Sigmoid model when applied with a multiplier to generate very fast infection rates becomes the Gompertz model. I stumbled into that observation using a version of the symmetrical Sigmoid model to run the US experience and applying a high multiplier to capture the metro NYC experience. The net effect was a Gompertz model driven experience.

[tonyblighe]

I'm geeking out over the fact that I am sitting at home with a tiny computer in my hand which allows me to watch a Stanford professor explain sigmoid and gompertz curves to me, and then lets me tell the world what I thought about it. I guess that means I'm old.

[tolex]

Thank you very much for these illuminating videos!

[christianlibertarian]

This is great. The Gompertz function is new to me, likely to more than just me.

[gabardjean-paul]

I love the font of your titles slides : which is it ?

[dagordon]

The Gompertz function was originally developed based on an actuary’s hypothesis, that older people are more likely to die than younger people. It’s interesting that that function can also fit microbe infections.

[jptrainor]

I tracked the Canadian confirmed case data as it evolved, using the publicly reported Canadian confirmed case data that stretched back to the first cases January. It clearly separated from exponential growth by the first week of April. Widespread distancing measures and "lock down" began in most of the country around March 15. It's easy to see the separation from pure exponential growth by fitting an exponential curve (k*exp(rt), derivative is r*k*exp(rt)) to both the cumulative confirmed cases data and the new case data. On a log plot the two curves are parallel if growth is purely exponential. They clearly were no longer parallel by end end of the first week of April - which is about where one would expect to see the effect of distancing and "lock down". I also tracked the data in one Canadian city, and one province each with populations of about one million people. The same pattern emerged of clear separation of from exponential growth a couple weeks after initiation of distancing measures.

[elephantwalkersmith]

What ode does this function reproduce?

[jacksoneglise]

Thank you do very much. The President should have been listening to you rather than doctor falchi.