Equivalent Forms of Exponential Equations | Chapter 7.1 | Learning Advanced Functions

Hello friend! In this video, we will learn how to change the base of any exponential expression! We will then use this procedure to help us solve a few exponential equations.

-=- Links -=-
7.1 Presentation

-=- Slide Information -=-
Change the Base of Powers
Exponential functions and expressions can be expressed in different ways by changing the base.
Changing the base of an exponential expression can be something like
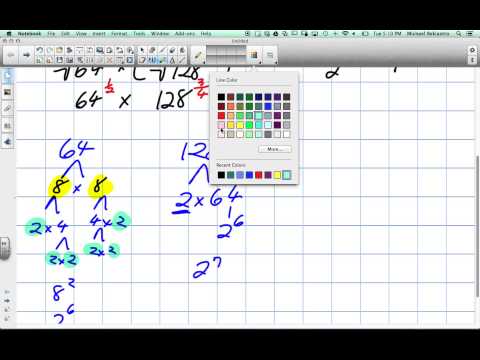
Changing 8 into 23
√9*(4√27)6 to 35.5
When we are presented with complex expressions like this we can start by taking them apart. √9 is the same as 31, (4√27)6 can be written as (4√33 )6, which can be written as (33/4)6, or 318/4. 31 times 318/4 equals 322/4. 322/4 is the same as 35.5.
13 to 3(log13/log3)
To transform 13 into something with the base of 3, we can set up an exponential equation, 3k = 13. We then can take log of both sides and so we get log 3k = log 13. Using the power-law we get k log 3 = log 13. Isolating for k we get k = log 13/log 3. So our answer is 3(log13/log3)
Using this procedure we can change any positive number as a power of any other positive number.

Solve an Equation by Changing the Base
Changing the base of one or more exponential expressions is a useful technique for solving exponential equations.
For example, let’s solve 25x-1 = 53x
We can express 25 as 52, so our equation is now (52)x-1 = 53x or 52x-2 = 53x
Since our bases are the same we can now just equate the exponents. 2x - 2 = 3x.
Collecting like terms we get -2 = x.
Let’s also solve 9k-1 = (√27)2k
We express 9 as 32 and 27 as 33, so our equation is now (32)k-1 = (√33)2k
Expanding we get 32k-2 = (33/2)2k or 32k-2 = 33k
Equating the exponents we get 2k - 2 = 3k, so -2 = k

Every exponential equation can be solved using technology.

-=-Hashtags-=-
#math #mathematics #grade12 #AdvancedFunctions #tutoring #University #HighSchool #trigonometry #UnitCircle #tutor #free #lesson #identities #equations #functions #graphing #transformations #reciprocal #exponents #logarithms #exponential #transformations #power #powerlaw #change #base #formula