filmov
tv
Dynamics - Lesson 13: Additional Relative Motion Problem

Показать описание
Top 15 Items Every Engineering Student Should Have!
This video is NOT sponsored. Some product links are affiliate links which mean if you buy something we'll receive a small commission.
Please consider supporting the channel by subscribing, commenting, and liking each video. This moves these videos up the search list and helps me greatly. Thank you for watching.
This video is copyrighted by the Jeff Hanson for the private use of our audience. Any other use of this video or any pictures, descriptions, or accounts of the video without written consent from Jeff Hanson is strictly prohibited.
Dynamics - Lesson 13: Additional Relative Motion Problem
Dynamics - Lesson 13 - Impulse Momentum Principle
Physics O-Level (5054) - (Mauritius / Ile Maurice)- MCQ on Dynamics -Lesson 13
Dynamics: Lesson 15 - Drawing Kinetic Diagrams, The Quintessential Dynamics Problem
Physics 20 Dynamics Lesson 13 Conservation of Mechanical Energy and Power
Dynamics - Lesson 11: Absolute Dependent Motion of Two Particles
Dynamics - Chapter 13 (1 of 2): Intro to Force and Acceleration
Dynamics - Lesson 12: Relative Motion with Translating Axis
DOCTOR Vs. NURSE: Education #shorts
Dynamics: Lesson 22 - Intro to Work in Dynamic Systems
What do you think is so special about System Dynamics? - John Sterman #shorts
NEWYES Calculator VS Casio calculator
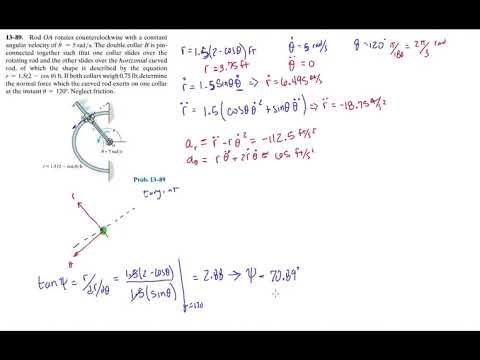
Problem 13-89 Dynamics Hibbeler 13th (Chapter 13) Engineering Dynamics
Left Turning Tendencies (Private Pilot Ground Lesson 13)
Dynamics: Lesson 18 - Equations of Motion Normal and Tangential Acceleration
Double Bass Drum Lesson 13 - Pedal Settings
Tough times Never last 😊✌️ #delhipolice #motivation
Problem F13-16 Dynamics Hibbeler 13th (Chapter 13) Engineering Dynamics
Physics Pulley Systems Part 1 Dynamics Lesson
Topper vs Average Student 😮 | Dr.Amir AIIMS #shorts #trending
Problem F13-1 Dynamics Hibbeler 13th (Chapter 13)
13-36 | Kinetics of a Particle | Chapter 13: Hibbeler Dynamics 14th ed | Engineers Academy
How To Play Like Tom Misch [Lesson 13 of 20] Tom Misch Guitar Lesson
Top 10 Toughest Exam In The World || Toughest Exam || #shorts #exam #test @aurfacts
Комментарии
 0:09:51
0:09:51
 0:21:03
0:21:03
 1:04:57
1:04:57
 0:14:42
0:14:42
 0:39:09
0:39:09
 0:19:18
0:19:18
 0:05:36
0:05:36
 0:13:40
0:13:40
 0:00:16
0:00:16
 0:13:59
0:13:59
 0:00:37
0:00:37
 0:00:14
0:00:14
 0:20:38
0:20:38
 0:05:37
0:05:37
 0:10:12
0:10:12
 0:12:16
0:12:16
 0:00:22
0:00:22
 0:11:15
0:11:15
 0:04:44
0:04:44
 0:00:25
0:00:25
 0:15:09
0:15:09
 0:13:50
0:13:50
 0:12:50
0:12:50
 0:00:29
0:00:29