Parametrizing and projecting a sphere | Universal Hyperbolic Geometry 38 | NJ Wildberger

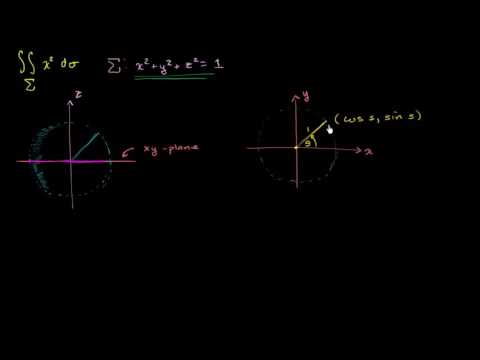
This video introduces stereographic and gnomonic projections of a sphere. We begin by reviewing three dimensional coordinate systems. A rational parametrization of a sphere is analogous to the rational parametrization of a circle found in MathFoundations29. Stereographic projection projects from the south pole of the sphere through the equatorial plane. Gnomonic projection projects from the center of the sphere through a tangent plane. Both are very important. Gnomonic projection works more naturally in the elliptic framework, where we identify antipodal points on a sphere.

Video Content:
00:00 Introduction
05:16 Stereographic projection
16:16 Recall parametrization of a circle
20:29 Algebraic underpinnings
22:42 Parametrization formula for a sphere
27:26 Spherical co-ordinates
30:34 Gnomonic projection
34:00 Gnomonic projection works more naturally with elliptic geometry

************************

Here are the Insights into Mathematics Playlists:

Here are the Wild Egg Maths Playlists (some available only to Members!)

************************

[bachirblackers]

Simply the best maths courses we have seen on youtube . Lovely smart simple explanation thanks prof .

[rolflang]

Thanks a lot for your this great intro.
I like the way you explain complicated things with some basic statements.

[pennyoflaherty]

Thankyou Proffessor Wildberger for Your presentations all the way through- I'm still inquisitive, they keep me going.
Trent O'Flaherty

[jehovajah]

Now I have seen this, it makes sense of your Quaternion explanation. You can generalise into 4 dimensions projecting a 3 dimensional space r, s, t onto the 4 dimensional surface x^2+y^3+z^2+w^2=1. Such a surface would be a spiral or Trochoid .

[سعیدعلیپور-هد]

Hello dr, How can I contact you regarding astronomical navigation issues?

[postbodzapism]

Really looking forward to your explanation on the rotations on the sphere.... from the viewpoint of rational trigonometry!

[pauluk]

You're right, there was no UHG37 (or perhaps its a place-holder for an even more important lecture to be given at a later date?)

Actually this lecture (wherever it lies in the series) was very good stand-alone material. The rational parametrization of the sphere to the plane and the connection to 'rational boxes'.

Thanks Norman.

[lmmgt]

thank you I like to see different ways to reflect a same problem. help me to review my high school stuff and spend some my retirement life. thanks YouTube too.

[vilbjrgbroch]

hello Norman Wildberger, it is clear that the parametrization of a sphere easily can be extended to a hypersphere (n-1)-sphere in n dimensions parametrized in a (n-1)-dimensional hyperplane. I am very interested in the relation between rotations and the rational parameters. Meaning the idea presented in Wildtrig15. I have used it a lot in audio-programming. I have written some python-scripts (using SymPy) which spit out the solution to problem posed in Wildtrig15 and also the same problem modified to e(t:u) from UHG-A12. It was easy to modify the script to try to find a similar relation for the 3-sphere and quaternion multiplication. It becomes a system of non-linear equations. Sympy can not find an answer and I am a bit stuck now not knowing whether this is because of SymPy or because there is no solution or if one need to add some human algebraic tricks. Have you looked at this problem or do you know of anyone who has. Thank you very much in advance. Vilbjørg

[jamesbra]

What if we do it with complex numbers? Can you solve Cauchy-Riemann?

[thomasolson]

The dot product does crazy stuff on your (3, 2, 5/2) example when the magnitude isn't 1. I assume I have to find the correct scalar to work with it. I'll take your example and put it on the sphere and I'm going to call it V2.
V2=(6/(sqrt(77), 4/sqrt(77), 5/sqrt(77))
V1=(1, 0, 0)
V3=(-5/77, 48/77, 60/77)
V4=(-5879/5929, -480/5929, -600/5929)

Dotproduct(V1, V2)=6/sqrt(77)
Dotproduct(V2, V3)=6/sqrt(77)
Dotproduct(V3, V4)=-5/77
Dotproduct(V1, V3)=-5/77

You can make a better sphere with 3 variables and they will all be rational. I guess that's like saying it's a parametrization of S3 on S2. Your example (2*r/(r^2+s^2+1), 2*s/(r^2+s^2+1), (-r^2-s^2+1)/(r^2+s^2+1)) is part of the following function when one of those variables is set to 1.
((-r^2-s^2+t^2)/(r^2+s^2+t^2), 2*t*s/(r^2+s^2+t^2), 2*t*r/(r^2+s^2+t^2))

It's a double angle function. The first double will be the same from V1, the second double will be a quadruple so it's hard to say what goes on after that. With these functions I can only get powers of two 2x, 4x, 8x, 16x. These multinomials have chebyshev polynomial properties.

I'll make a video tomorrow talking about it.

[richiedon]

When might it be more advantageous to use spherical coordinates, I wonder.

[greg]

If you know the RADIUS and the CIRCUMFERENCE (like Earth's)...   Earlier videos you claim that the classical formulas are a bit shady...   What is a formula that calculates the (per) planar circular section at 90 degrees to the radius through the process (planar circle) down to the axis (essentially the curve drop at 90 degrees to the radius)...  as I've used many formulas and with larger number values and they don't seem to equate properly.   The formulas I'm using are measuring the M.O./BULGE value...  what is a formula at 90 degrees to the radius in relation to circumference.    RATIO of the Radius and Circumference says 2086 feet per 1 km of curve (but I think that is just creating a diamond/linear line to the other axis).  I haven't engaged in such math for about 35 years.   The formulas they use on the web don't make sense with larger numbers.