filmov
tv
Coin Game \ Magic Trick \ Maths: The Penney Ante Part 2 (Re: Derren Brown: How to Win the Lottery)
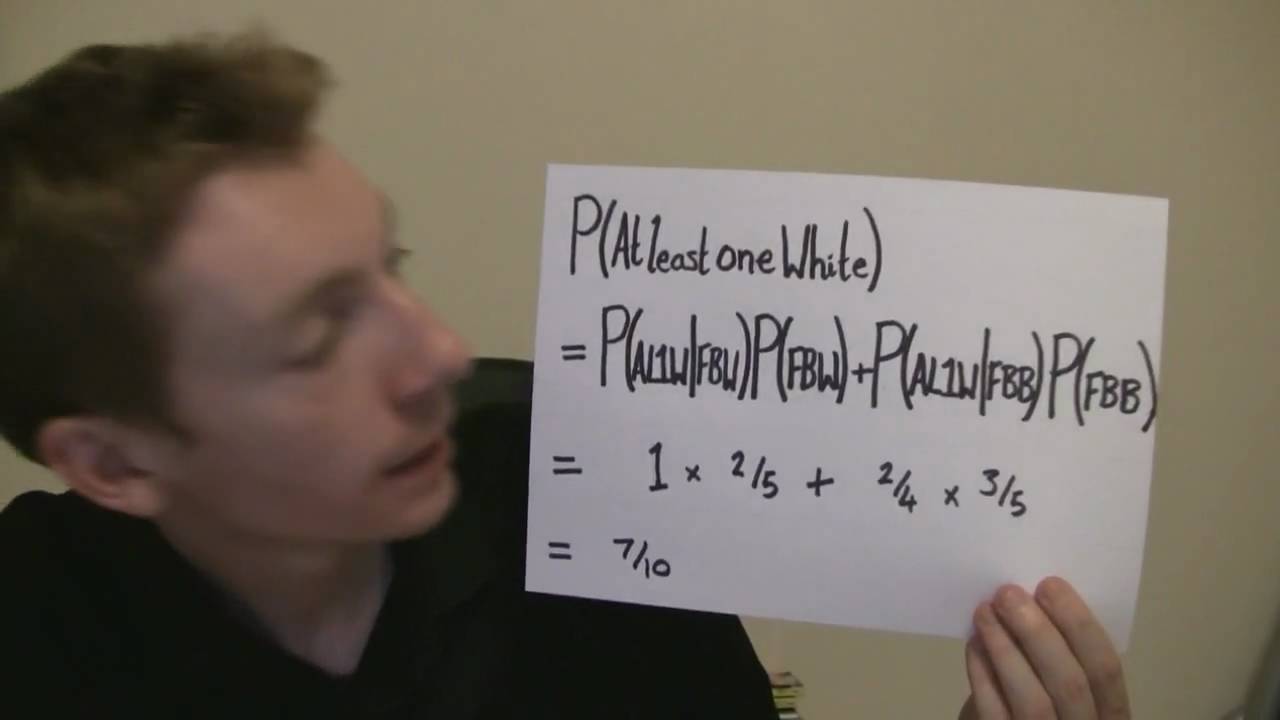
Показать описание
Penney Ante is a coin game devised in 1969 by a mathematician called Walter Penney. In it, two players predict three coin tosses. The prediction that appears first in a run of coin tosses wins. This should be a fair game. However, if Player 2 makes his prediction after Player 1, he can use mathematics and probability to increase his chances of winning.
On Wednesday 9th of September 2009 (09-09-09) UK magician Derren Brown predicted the national lottery numbers on live TV. The following Friday he explained how he did it. This included a demonstration of the Penney Ante.
On Wednesday 9th of September 2009 (09-09-09) UK magician Derren Brown predicted the national lottery numbers on live TV. The following Friday he explained how he did it. This included a demonstration of the Penney Ante.
Dynamic Coins from Marvin's Magic
The coin trick that fools magicians! TUTORIAL #shorts
HARD MODE Coin Vanish 🪙👀 #shorts
Flying Coins [Magic Trick] - Unboxing
Amazing Tutorial Coin Magic Trick #youtubeshorts #viral #trending #art #magic #tricks #shorts
Anti-Gravity Coin Trick #magic
The Shell Game (Magic Trick Explained)
2 EUro Coin In Bottle Magic Trick Gimmick Coin Game
Alakazam Review Show Ep 19 | Six Sided Psychic, HedEx & Poker Packet Trick
Bar Tricks: The Coin Snatch
JW Grip Coin Vanish #coinmagic
The Best, Fairest Coin Flip Cheat Ever (Thanks to Rick Smith Jr.)
How to teleport coins / magic trick #shorts
10 IMPOSSIBLE Coin Tricks Anyone Can Do | Revealed
The Touchy Quarter Alignment
Coin Game \ Magic Trick \ Maths: The Penney Ante Part 1 (Re: Derren Brown: How to Win the Lottery)
8 SIMPLE Coin Tricks Anyone Can Do | Revealed
Coin Through Glass Magic Trick 😳 #shorts
Revealed Coin Vanishes Magic Trick - #shorts
COIN HEAD AND TAIL TRICK - DO YOU KNOW, HOW || #shorts
Visual COIN TRICK - TUTORIAL | TheRussianGenius
Coin Game \ Magic Trick \ Maths: The Penney Ante Part 2 (Re: Derren Brown: How to Win the Lottery)
The BEST Coin Vanish In The World | Revealed
Learning to COIN ROLL in a day
Комментарии
 0:01:33
0:01:33
 0:00:41
0:00:41
 0:00:40
0:00:40
 0:01:51
0:01:51
 0:00:32
0:00:32
 0:00:43
0:00:43
 0:02:37
0:02:37
 0:01:21
0:01:21
 0:26:54
0:26:54
 0:01:00
0:01:00
 0:00:32
0:00:32
 0:06:05
0:06:05
 0:00:39
0:00:39
 0:13:21
0:13:21
 0:02:12
0:02:12
 0:03:47
0:03:47
 0:11:48
0:11:48
 0:00:09
0:00:09
 0:00:34
0:00:34
 0:00:25
0:00:25
 0:06:23
0:06:23
 0:08:26
0:08:26
 0:07:44
0:07:44
 0:00:39
0:00:39