filmov
tv
Sum of the squares of 'n' Consecutive integers - Simple Proof
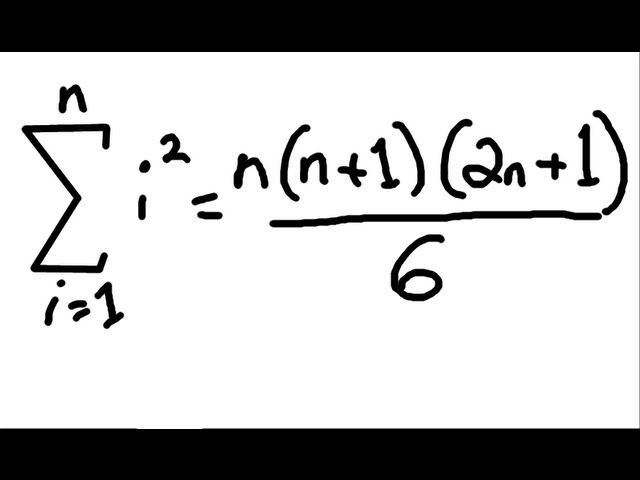
Показать описание
In this video I show the proof for determining the formula for the sum of the squares of "n" consecutive integers, i.e. 1^2 + 2^2 + 3^2 +.... + n^2. This is a pretty abstract proof and makes use of the useful "telescoping" or collapsing sum which I illustrate in the video. The formula for the sum of squares comes up very often in calculus so it's a good idea to understand the proof!
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
Sum of n squares | explained visually |
Sums of Sums of Squares (visual proof)
Sum of Squares I (visual proof)
Find the sum of first n squares, difference equation approach, (ft. Max!)
The Square-Sum Problem - Numberphile
Finding the sum of n squares part 1
Decomposition of Variability: Sum of Squares | Statistics Tutorial
Factoring sum of squares | Imaginary and complex numbers | Precalculus | Khan Academy
Class 9 Math Exercise 5.1 Complete || 9 Class Mathematics Exercise 5.1 Question No.1 To 5
Sum of Squares Computational Formula
Sum of Squares Visual Proofs: From Level 1 to Level 5
Visual Sum of Squares III (proof without words)
ANOVA 1: Calculating SST (total sum of squares) | Probability and Statistics | Khan Academy
Sum of squares
Summing Squares Geometrically
Sum of Squares II (visual proof)
Number Theory | Sums of Squares Part 1.
Factor a Sum of two Squares (visual proof)
Sum of the squares of 'n' Consecutive integers - Simple Proof
Extra Sum of Squares Regression and Reduced Sum of Squares Residual
Sum of squares between
Sum of Squares: Computational Formula
Can You Find the Sum of Squares of this Series? | Step-by-Step Tutorial
Formula for the Sum of Squares of Consecutive Odd Integers : Science & Math
Комментарии
 0:02:14
0:02:14
 0:05:18
0:05:18
 0:01:38
0:01:38
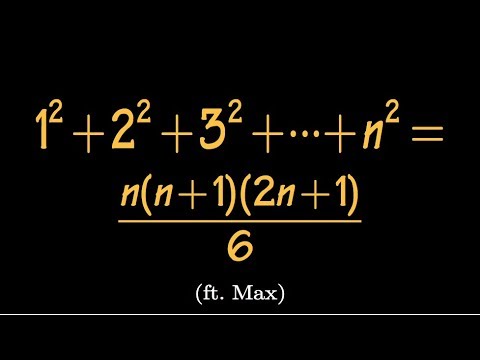 0:11:19
0:11:19
 0:09:07
0:09:07
 0:06:16
0:06:16
 0:03:20
0:03:20
 0:04:51
0:04:51
 0:22:08
0:22:08
 0:04:55
0:04:55
 0:03:22
0:03:22
 0:02:27
0:02:27
 0:07:39
0:07:39
 0:04:08
0:04:08
 0:00:56
0:00:56
 0:02:25
0:02:25
 0:06:37
0:06:37
 0:01:42
0:01:42
 0:11:40
0:11:40
 0:15:59
0:15:59
 0:03:46
0:03:46
 0:03:51
0:03:51
 0:04:57
0:04:57
 0:03:38
0:03:38