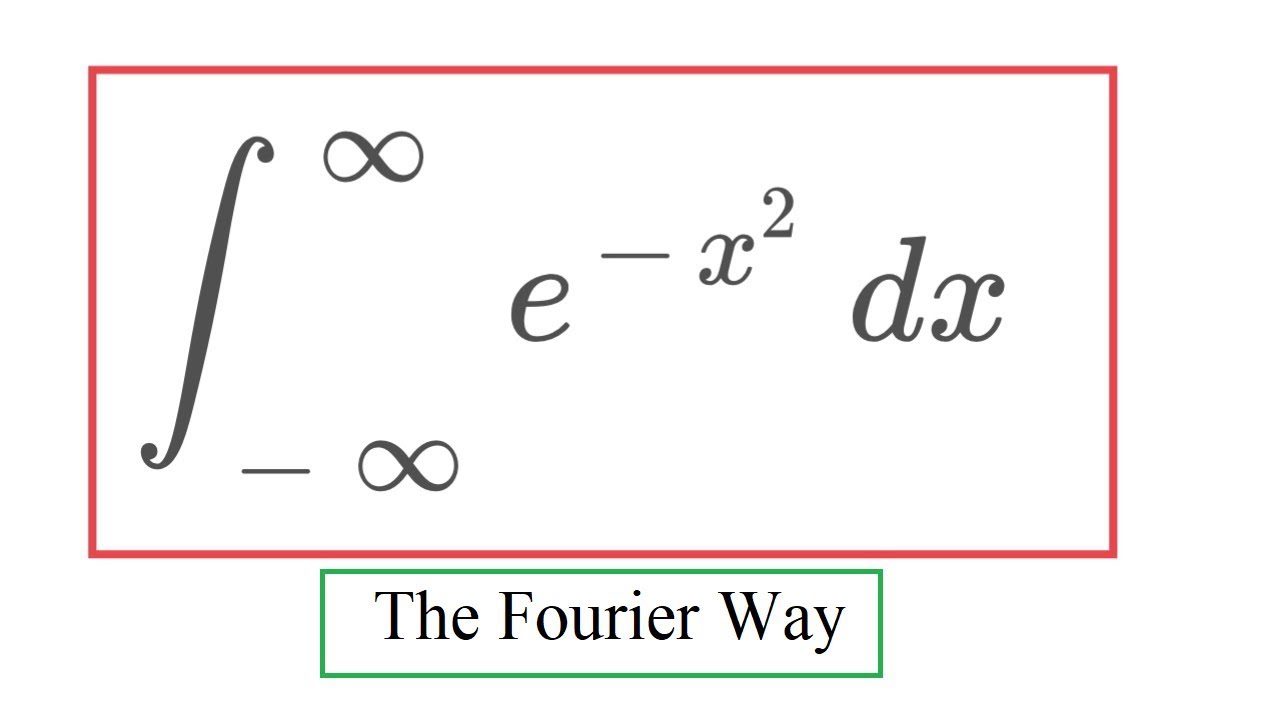
Gaussian Integral 10 Fourier Way

Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out!

In this video, I show how the Gaussian integral appears in the Fourier transform: Namely if you take the Fourier transform of the Fourier transform of f, you get 2pi f(-x), and I show how that 2pi relates to the Gaussian integral. At the same time, I calculate the Fourier transform of e^-ax^2 and show that this class of functions plays the analog of e^x in differential equations

[saatee]

Dear sir, the angle of the camera is a bit off and at times writings is not that clear.
Anyway I enjoy this video.

[tylershepard]

We use the Fourier transform in electromagnetism to help us solve the wave equation. Turns out the Fourier transform of the Wave Equation with respect to time is called the Helmholtz Equation. This is where the results for diffraction and interference come from.

[BRORIGIN]

Im really on edge today. Is this a real integral or an april fools joke? I mean, how can it be that pretty and still correct? There has to be a divide by 0 mistake somewhere?
Right?
No?
Ok

[achyuthramachandran]

After showing integral K = √(2π), you can make a substitution in K - namely, let u = x ÷ √2. Some algebra later, you end up with √(2π) = √2 • Gaussian integral => Gaussian integral = √π

[ignaciomoralesgil]

I still doubt about the equality around 10:09, for all functions beyond it depend on z, but I'm not sure that fiesta equality would work with the first f being a function of z

[Rundas]

Using fourier transform to solve differential equations and using a differential equation to find a fourier
Looks like some kind of mathematical perpetual machine to me :D
And also I expected something less serious like the -1/12-th way of solving the gaussian integral: wolfram-alpha

Everything is possible on 04/01.

[jonasdaverio]

I made my A-levels job (in Switzerland it's called "Travail de maturité" or "Maturaarbeit", Matura=Abitur in Switzerland) on using the discrete Fourier transform for numerically integrating differential equations, haha. The term that you have to divide the Fourier transform by is a sum of e^iksi instead of ksi when you discretise your frequency domaine, haha (if I remember well)

[cristianperez]

Great video ! Im subscribe !! But i have a question, how to multiply series ?? Do you have a example ?

[dgrandlapinblanc]

Very hard for me. Very impressive. I've finished the "pack" gaussian integral. Thank you very much.

[narutosaga]

Dr Peyam, لطفا زاویه دوربین را تغییر دهید :)

[がつかくん]

Gaussian project by Dr.peyam is nearing the end game.
I'm a little bit sad about that.