filmov
tv
How to Integrate with Cauchy's Derivative Formula
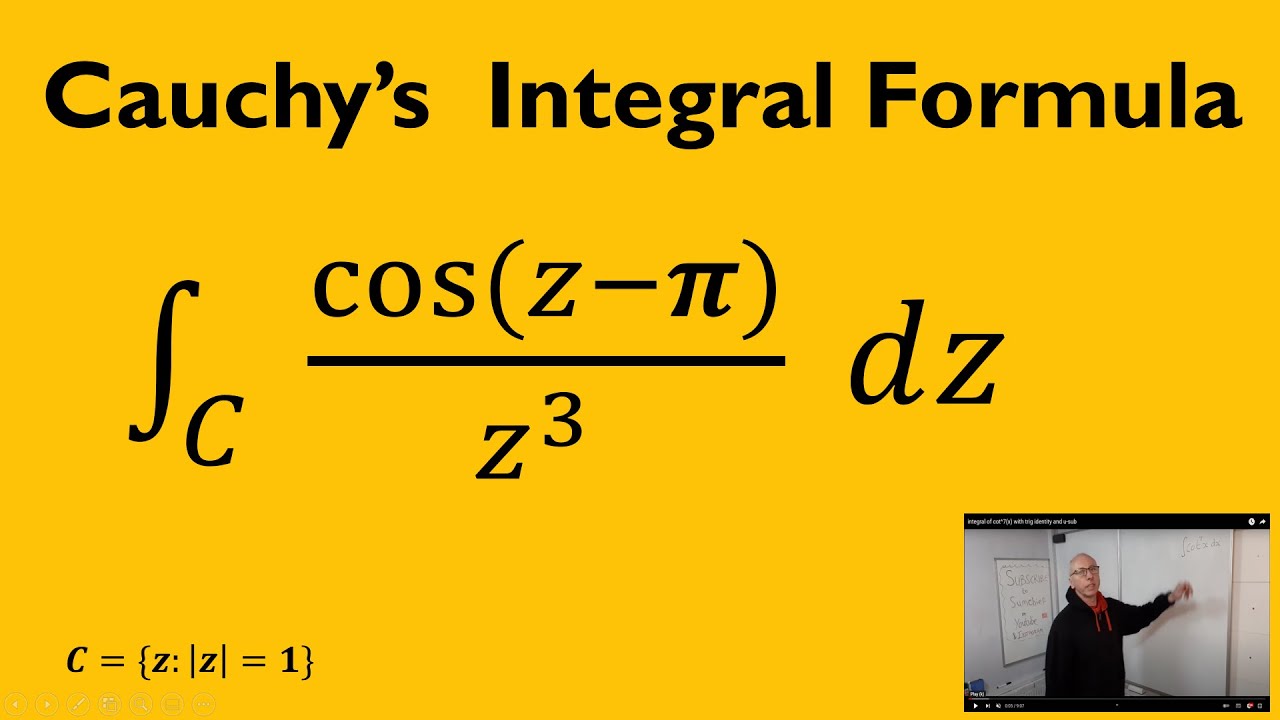
Показать описание
This video shows how to use Cauchys Derivative Formula .
Complex Analysis here where z=x+iy .
Its a neat way of integrating without actually doing any integration .
First see that the integral is set in a Simple Closed Contour which can be set in a simply connected contour . We set C={z:|z|=1} and R=Complex Plane .
the numerator has cos (z-pi) and z^3 in the denominator.
Then we find the simple poles of the function being integrated , and see if they are in the regions specified . If they are outside of the closed contour then they amount to 0 by Cauchys Integral Formula . The ones inside are left which become of interest .
Then we calculate the function as z approaches zero which is the same as eliminating the singularity we are interested in , and multiply by 2i pi .
The second derivative of cos(z-pi) is the only tricky part , and not forgetting the k=n-1 for the factorial value .
#algebra
#complex
#maths
#cauchy
#calc3
#calculus
#analysis
#mathematics
#mathstrick
#calcio
#calculo
Complex Analysis here where z=x+iy .
Its a neat way of integrating without actually doing any integration .
First see that the integral is set in a Simple Closed Contour which can be set in a simply connected contour . We set C={z:|z|=1} and R=Complex Plane .
the numerator has cos (z-pi) and z^3 in the denominator.
Then we find the simple poles of the function being integrated , and see if they are in the regions specified . If they are outside of the closed contour then they amount to 0 by Cauchys Integral Formula . The ones inside are left which become of interest .
Then we calculate the function as z approaches zero which is the same as eliminating the singularity we are interested in , and multiply by 2i pi .
The second derivative of cos(z-pi) is the only tricky part , and not forgetting the k=n-1 for the factorial value .
#algebra
#complex
#maths
#cauchy
#calc3
#calculus
#analysis
#mathematics
#mathstrick
#calcio
#calculo
 0:16:43
0:16:43
 0:40:45
0:40:45
 0:09:27
0:09:27
 0:05:38
0:05:38
 0:09:05
0:09:05
 0:16:41
0:16:41
 0:22:16
0:22:16
 0:00:15
0:00:15
 0:09:39
0:09:39
 0:10:16
0:10:16
 0:11:00
0:11:00
 0:18:54
0:18:54
 0:09:20
0:09:20
 0:20:42
0:20:42
 0:10:47
0:10:47
 0:04:10
0:04:10
 0:16:35
0:16:35
 0:12:06
0:12:06
 0:04:22
0:04:22
 0:05:10
0:05:10
 0:08:09
0:08:09
 0:07:50
0:07:50
 0:03:41
0:03:41
 0:09:28
0:09:28