Equation on Symmetric Polynomials | Balkan MO 2017

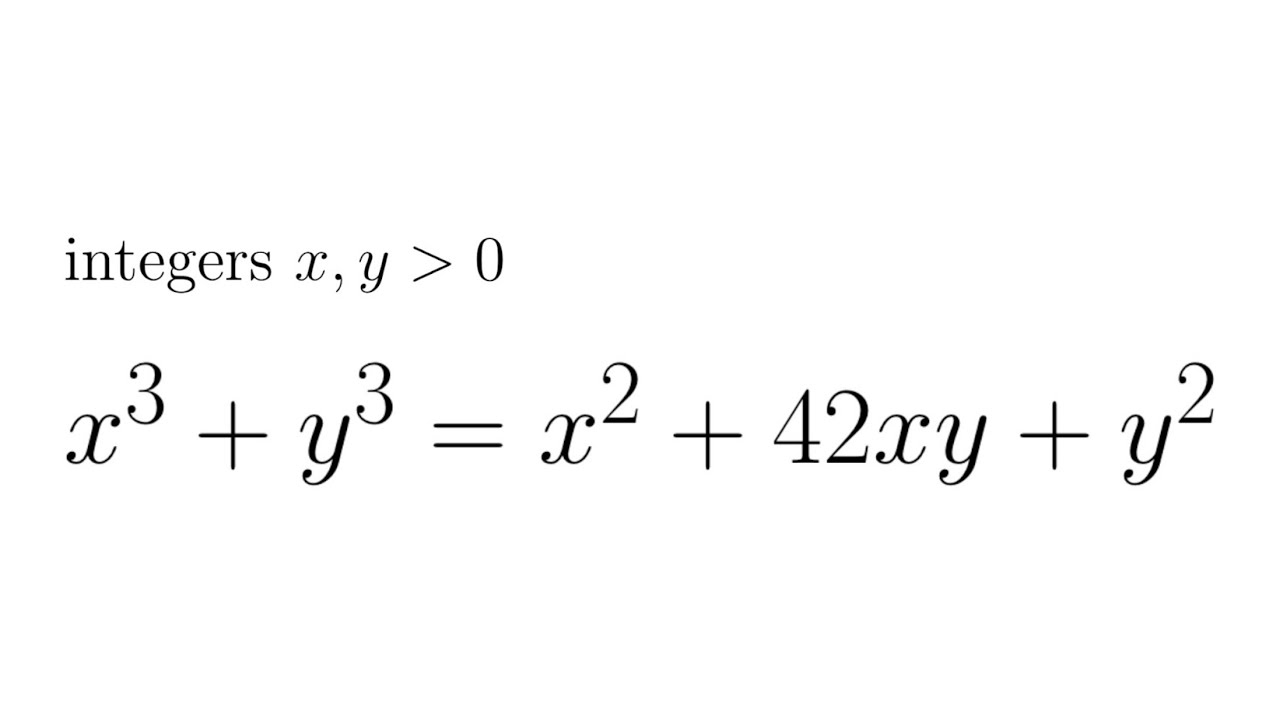
preview_player
Показать описание

  1. letsthinkcritically
Рекомендации по теме
Equation on Symmetric 0:09:43

Equation on Symmetric Polynomials | Balkan MO 2017

Symmetric Polynomials and 0:18:23

Symmetric Polynomials and Polynomial Manipulations - Mastering AMC 10/12

Vietta's formulas, Symmetric 0:10:17

Vietta's formulas, Symmetric polynomials

Solving the Most 0:28:18

Solving the Most Ridiculous Systems of Equations (ft. a cool theorem) #some3

Symmetric polynomials 3 0:16:20

Symmetric polynomials 3

Prelude to Galois 0:32:34

Prelude to Galois Theory: Exploring Symmetric Polynomials

Grade 10 - 0:04:31

Grade 10 - Algebra - Homogeneous and symmetric polynomials

solving this in 0:03:44

solving this in a clever way | symmetric polynomial equations

Elementary Symmetric Polynomials 0:04:51

Elementary Symmetric Polynomials Used To Factor A Six Term Expression, x^2 + y^2 + 2xy + 4x +4y - 21

Newton's Identity, Lesson 0:15:30

Newton's Identity, Lesson 5: Symmetric Polynomials of Roots and Elementary Symmetric Polynomial...

Use symmetric polynomials 0:06:02

Use symmetric polynomials to solve a radical equation (I)

Use symmetric polynomials 0:07:04

Use symmetric polynomials to solve a radical equation (II)

Symmetric polynomials: definition 0:31:09

Symmetric polynomials: definition and examples

Symmetric polynomial 2 0:19:44

Symmetric polynomial 2

Week 9-Lecture 44 0:30:10

Week 9-Lecture 44

Symmetric Functions of 0:06:02

Symmetric Functions of Roots of a Quadratic Equation | SHS 1 ELECTIVE MATH

Use symmetric polynomials 0:06:26

Use symmetric polynomials to solve a Diophantine equation: An HMMT problem

Elementary Symmetric Polynomials 0:10:34

Elementary Symmetric Polynomials Playing the Role of a Factoring Transform for 10 term Expression

Week 9-Lecture 45 0:30:42

Week 9-Lecture 45

What Is A 0:02:23

What Is A Symmetric Polynomial? - 2 Minute Math with Laura Colmenarejo

2nd degree Elementary 0:08:33

2nd degree Elementary Symmetric Polynomials(ESPs) helps solve this 5th power system of Equations

Poster Child System 0:10:21

Poster Child System of Equations ready to be abused by Elementary Symmetric Polynomials(ESPs)

Non-Linear System of 0:08:31

Non-Linear System of Equations Eviscerated by Elementary Symmetric Polynomial Substitutions

College Algebra: Symmetric 0:11:13

College Algebra: Symmetric Functions

Комментарии
Автор

I love these positive integer problems.

richardfredlund
Автор

GCD of two numbers can be one of the numbers. That means X, or Y can be 1. In which case, you could divide and get an integer.

bollyfan
Автор

Thnku sir Thnku sir Thnku sir Thnku sir Thnku sir Thnku sir Thnku sir Thnku sir Thnku sir

SuperYoonHo
Автор

What about X, Y = 6, 7 / 7, 6? It doesn't give us a solution, but I think it should still be mentioned. We get 13d=1+43*42/(49-42+36)=43, which is not divisible by 13.

maxbow-arrow
Автор

beautiful how do you notice the fact that Y^2 can be only 1 in the first case, I didnt realize that! great explanation :)

pablomartinezgonzalez
Автор

I modified the given equation to (x^2-xy+y^2)(x+y-1)=43xy. Then I analysed this in a similar way leading to the same answer.

ansisozolins
Автор

Pongo s=x+y, p=xy, risulta p=(s^3-s^2)/3s+40, e l'unica soluzione intera è 1, 7 e 7, 1 con s=8, p=7

giuseppemalaguti
Автор

Why do you limit to strictly positive integers ? Beside the trivials (0, 0) and (0, 1), there is also an interesting (1, -6)

tontonbeber
Автор

Comment prouver que XY et X^2_XY+Y^2sont copremiers?

hamzalouliditv