filmov
tv
Elementary Symmetric Polynomials Playing the Role of a Factoring Transform for 10 term Expression

Показать описание
Difficult to factor expression x^3 + y^3 +2xy^2 + 2x^2y + 2y^2 + 2x^2 + xy - x - y + 6 was transformed to a function of sigma1 and sigma2. Subscripted sigma notation. After it was factored as a function of ESPs (x+y) and xy sigma 1 and sigma 2 respectively, it was converted back to its x y variable complete factored form via the substitution sigma 1 equals (x+y) and sigma 2 equals the product xy
@mathiscool1292 expressed interest in this fascinating occasional math olympiad topic and also the notion of complete.
Fundamental theorem of symmetric polynomials essentially states that a symmetric polynomial has a unique factorization in terms of the Elementary Symmetric Polynomials which can be transformed back to the original variables of the original polynomials. In short ESPs are excellent factoring aids! Subscripted sigma notation typically used to represent ESPs. Not Extra Sensory Perception!!
The publications and work of Hamza Elhadi S. Daoub is considered mathematically seminal.
Keith Conrad defined a polynomial to be symmetric if it
is unchanged by all permutations of its variables. Unfortunately, the term "unchanged" is ambiguous.
Lynchburg, VA mathematician James Cook related this to fixed fields, splitting fields, automorphisms and permutation groups in an abstract algebra 2 course in Spring of 2018.
A Potpourri of Algebra
Khor Shi-Jie( Hwa Chong Institution trained scholar and preeminent Google Software engineer) did a great example of this helping competitors prepare for various Math Olympiads.
March 27, 2012
A fascinating side note is the research being done on the necessary and sufficient conditions for the concavity of the sum of an arbitrary number of ESPs by Xavier Lachaume. Not sure if it is always concave up or down related to the second derivative of the finite sum. It seems connected to Einstein's curved space speculations! Interesting Stuff!!!
@mathiscool1292 expressed interest in this fascinating occasional math olympiad topic and also the notion of complete.
Fundamental theorem of symmetric polynomials essentially states that a symmetric polynomial has a unique factorization in terms of the Elementary Symmetric Polynomials which can be transformed back to the original variables of the original polynomials. In short ESPs are excellent factoring aids! Subscripted sigma notation typically used to represent ESPs. Not Extra Sensory Perception!!
The publications and work of Hamza Elhadi S. Daoub is considered mathematically seminal.
Keith Conrad defined a polynomial to be symmetric if it
is unchanged by all permutations of its variables. Unfortunately, the term "unchanged" is ambiguous.
Lynchburg, VA mathematician James Cook related this to fixed fields, splitting fields, automorphisms and permutation groups in an abstract algebra 2 course in Spring of 2018.
A Potpourri of Algebra
Khor Shi-Jie( Hwa Chong Institution trained scholar and preeminent Google Software engineer) did a great example of this helping competitors prepare for various Math Olympiads.
March 27, 2012
A fascinating side note is the research being done on the necessary and sufficient conditions for the concavity of the sum of an arbitrary number of ESPs by Xavier Lachaume. Not sure if it is always concave up or down related to the second derivative of the finite sum. It seems connected to Einstein's curved space speculations! Interesting Stuff!!!
Комментарии
 0:10:34
0:10:34
 0:15:30
0:15:30
 0:32:34
0:32:34
 0:07:53
0:07:53
 0:04:51
0:04:51
 0:26:24
0:26:24
 0:10:17
0:10:17
 0:16:20
0:16:20
 0:18:23
0:18:23
 0:08:33
0:08:33
 0:10:21
0:10:21
 0:00:42
0:00:42
 0:09:11
0:09:11
 0:31:09
0:31:09
 0:07:58
0:07:58
 0:30:10
0:30:10
 0:26:58
0:26:58
 0:28:18
0:28:18
 0:19:44
0:19:44
 0:35:26
0:35:26
 0:08:31
0:08:31
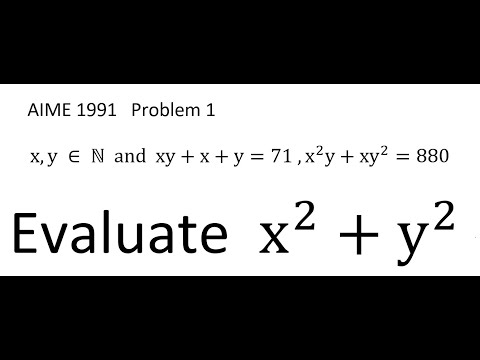 0:05:54
0:05:54
 0:00:42
0:00:42
 0:02:23
0:02:23