filmov
tv
Find the limit of (1+2+3+...n)^(1/n) as n goes to infinity

Показать описание
In this video we use L'Hôpital's rule to calculate the limit of the sum of n numbers raised to 1/n as n goes to infinity!
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
Find the Limit of SUM((1/n^3)(i - 1)^2) as n approaches infinity
Determine if sequence converges or diverges, if converges find limit {(1+ 2/n)^n}
Write the value of lim n to infinity 1+2+3+...+n/ n^2|CBSE|NCERT|TERM 1|LIMITS|RD SHARMA|VSAQ|2021
Find the limit of (1+2+3+...n)^(1/n) as n goes to infinity
Limit at Infinity / Indeterminate form 1 to Infinity (How to find)
Lim (1+1/n)^n as n tends to infinity ?? # Trick
Find the limit of 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/6n as n tends to infinity
Solving 100 QUESTIONS on all things SEQUENCES & SERIES! - PART 2 | Math with Professor V
❖ Finding the Limit of a Sequence, 3 more examples ❖
Converging and Diverging Sequences Using Limits - Practice Problems
lim (1+2^1/2+...........n^1/n)/n|| short trick for limits
Evaluate: Lim(n→∞)[{(1+1/n)(1+2/n)(1+3/n)........(1+n/n)}^1/n]
lim n tends to infinity (1/1+n + 1/2+n + 1/3+n+......+1/2n) is equal to #iitjeemains2023
How to Prove that the Limit of (2n + 1)/(3n + 7) as n approaches infinity is 2/3
Summation Formulas You Need to Know #Shorts #math #maths #mathematics
Convergence and Divergence - Introduction to Series
EVALUATE: lim(n→∞) [(1+1/n)^1/1.(1+2/n)^1/2.(1+3/n)^1/3........(1+n/n)^1/n]
Limit of 3^n/n! as n approaches infinity
EVALUATE: Lim(n→∞)[1/n+1/(n+1)+1/(n+2)+......+1/3n]
lim (n-›∞) [(1+1/n)(1+2/n)(1+3/n)... (1+n/n)]^(1/n)
Sequences | Convergence and Divergence
Use the Limit Comparison Test to determine convergence or divergence of 2^n/(3^n+1)
Determine the limit of the sequence {sqrt(n^2 + 3n) -n}. Multiply by conjugate
Комментарии
 0:07:50
0:07:50
 0:06:29
0:06:29
 0:03:21
0:03:21
 0:01:21
0:01:21
 0:03:08
0:03:08
 0:17:26
0:17:26
 0:00:22
0:00:22
 0:01:05
0:01:05
 3:05:07
3:05:07
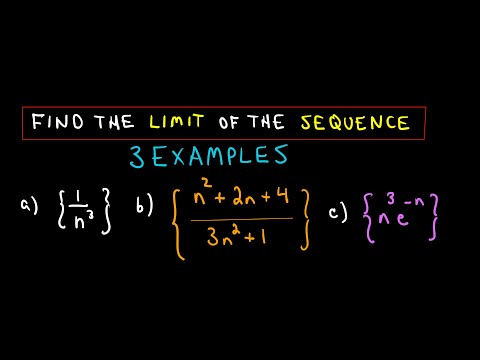 0:03:24
0:03:24
 0:30:13
0:30:13
 0:03:13
0:03:13
![Evaluate: Lim(n→∞)[{(1+1/n)(1+2/n)(1+3/n)........(1+n/n)}^1/n]](https://i.ytimg.com/vi/-700ZRmhDuA/hqdefault.jpg) 0:06:36
0:06:36
 0:03:40
0:03:40
 0:11:39
0:11:39
 0:00:20
0:00:20
 0:16:18
0:16:18
![EVALUATE: lim(n→∞) [(1+1/n)^1/1.(1+2/n)^1/2.(1+3/n)^1/3........(1+n/n)^1/n]](https://i.ytimg.com/vi/NqV136R3vGk/hqdefault.jpg) 0:07:56
0:07:56
 0:01:22
0:01:22
![EVALUATE: Lim(n→∞)[1/n+1/(n+1)+1/(n+2)+......+1/3n]](https://i.ytimg.com/vi/eR_0XG_M2ik/hqdefault.jpg) 0:03:34
0:03:34
 0:07:14
0:07:14
 0:27:54
0:27:54
 0:03:12
0:03:12
 0:03:49
0:03:49