filmov
tv
Riemann sums and sigma notation

Показать описание
Understanding how Riemann sums can result in "negative area"
Riemann sums and sigma notation
Riemann Sums in Sigma Notation
Riemann Sums - Left Endpoints and Right Endpoints
Calculus AB/BC – 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
Worked example: Riemann sums in summation notation | AP Calculus AB | Khan Academy
Finding The Area Using The Limit Definition & Sigma Notation
Summation Formulas and Sigma Notation - Calculus
Region, Riemann sum, and integral!
Riemann sums in summation notation | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Summation Formulas You Need to Know #Shorts #math #maths #mathematics
Definite integral as the limit of a Riemann sum | AP Calculus AB | Khan Academy
Riemann Sums Video 1 - Sigma Notation
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
LT 23 - Riemann Sums using Summation Notation
CALC 6 4 Riemann Sums and Sigma Notation
Converting a Riemann Sum to a Definite Integral
Riemann sum notation
Day 58 More practice with Riemann Sums and Sigma Notation
Lesson 23 Riemann Sums in Sigma Notation
Sigma Notation and Summation Notation
Summation notation for Riemann Sums in integration | Calculus (integration)
Riemann Sums - How to use Sigma Notation
Riemann Sums in Sigma Notation
Lecture 7 (Part 4): Definite integral as Riemann Sum; Sigma (summation) notation with properties
Комментарии
 0:06:36
0:06:36
 0:04:56
0:04:56
 0:20:10
0:20:10
 0:21:07
0:21:07
 0:07:07
0:07:07
 0:13:18
0:13:18
 0:20:24
0:20:24
 0:00:30
0:00:30
 0:08:31
0:08:31
 0:00:20
0:00:20
 0:04:26
0:04:26
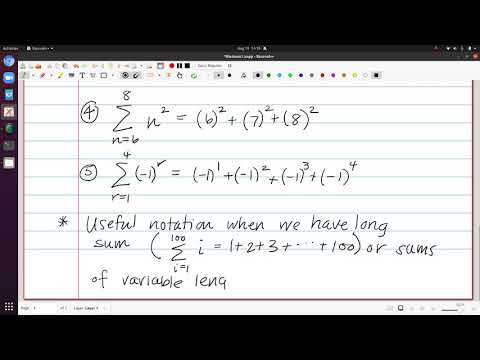 0:13:39
0:13:39
 0:13:18
0:13:18
 0:04:54
0:04:54
 0:20:39
0:20:39
 0:03:13
0:03:13
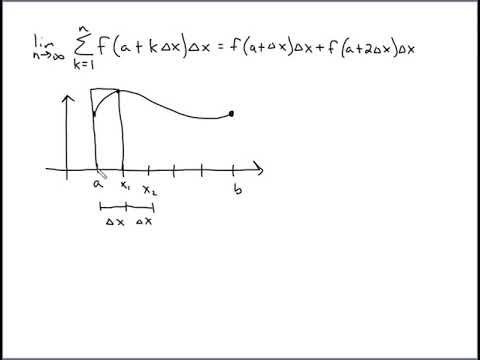 0:07:40
0:07:40
 0:21:05
0:21:05
 0:14:22
0:14:22
 0:15:41
0:15:41
 0:05:07
0:05:07
 0:06:34
0:06:34
 0:12:20
0:12:20
 0:30:30
0:30:30