filmov
tv
Taylor series for e^x, Single Variable Calculus
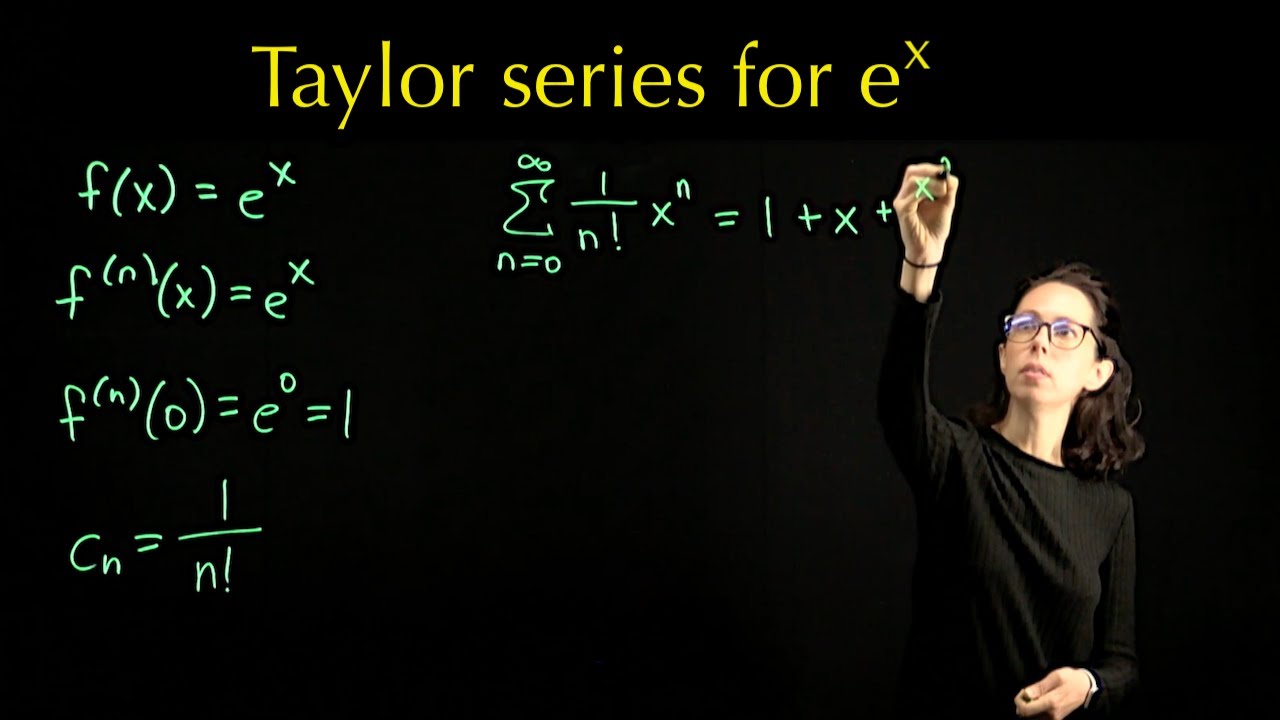
Показать описание
We find the Taylor series (or Maclaurin series) for f(x)=e^x by computing the coefficients and the radius of convergence. Since the derivative of 𝑒^𝑥 is 𝑒^𝑥 itself, 𝑓^{(𝑛){(0)=𝑒^0=1. Therefore, each Taylor coefficients 𝑐𝑛 is 1/𝑛!, and the Maclaurin Series for 𝑒^𝑥 is e^x = Σ x^n/n!, beginning with n=0.
Using the "coefficients only" version of the ratio test, we establish that the radius of convergence is infinite, so the series is valid for all real numbers.
We then use this to tackle an integral that we cannot do by hand (in terms of elementary functions). This lecture is part of my course on Single Variable Calculus.
#mathematics #math #calculus #sequencesandseries #powerseries #taylorseries #maclaurinseries #iitjammathematics
Using the "coefficients only" version of the ratio test, we establish that the radius of convergence is infinite, so the series is valid for all real numbers.
We then use this to tackle an integral that we cannot do by hand (in terms of elementary functions). This lecture is part of my course on Single Variable Calculus.
#mathematics #math #calculus #sequencesandseries #powerseries #taylorseries #maclaurinseries #iitjammathematics
Taylor series for e^x, Single Variable Calculus
How To Calculate The Taylor Expansion of e^x?
Taylor series | Chapter 11, Essence of calculus
Ex: Find the Taylor Series of e^x
Taylor Series and Maclaurin Series - Calculus 2
Taylor Series ex 1
Maclaurin Expansion log(1+e^x)
Taylor and Maclaurin Series
Derivatives (Week-5 session-2 M1ES)
Intro to Taylor Series: Approximations on Steroids
Find e^-x^2 as a Taylor Polynomial at 0
Taylor Series Ex #1 f(x)= sqrt(1+2x)
Maclaurin Series for e^x (Calculus 2)
Ex: Find a Degree One and Degree Two Maclaurin Polynomial
Find coefficient in Taylor series - ex. 1
Taylor series for ln(1+x), Single Variable Calculus
3 Applications of Taylor Series: Integrals, Limits, & Series
Find a Taylor series generated by function f(x) = e^(x/2) at point x = 2
Common Taylor Series (Calculus II Tutorial) - Derivations, Example Problems (sinx, cosx, e^x, 1/1-x)
Find the Taylor series generated by f(x) = e^x at x = 2
Benson Boone met his ex girlfriend from middle school during a concert 😂
Taylor's Series Expansion of One Variable
MILEY CYRUS Sings NEW SONG In Front Of Her Ex-Husband LIAM HEMSWORTH | #MileyCyrus #Shorts
Ex: Find the Taylor Series of x^3
Комментарии
 0:13:15
0:13:15
 0:08:19
0:08:19
 0:22:20
0:22:20
 0:05:59
0:05:59
 0:29:22
0:29:22
 0:05:16
0:05:16
 0:08:12
0:08:12
 0:09:34
0:09:34
 1:21:46
1:21:46
 0:12:43
0:12:43
 0:06:39
0:06:39
 0:05:24
0:05:24
 0:03:34
0:03:34
 0:05:09
0:05:09
 0:02:42
0:02:42
 0:10:53
0:10:53
 0:07:22
0:07:22
 0:04:22
0:04:22
 0:29:40
0:29:40
 0:02:30
0:02:30
 0:00:37
0:00:37
 0:46:19
0:46:19
 0:01:00
0:01:00
 0:06:07
0:06:07