Taste of topology: Open Sets

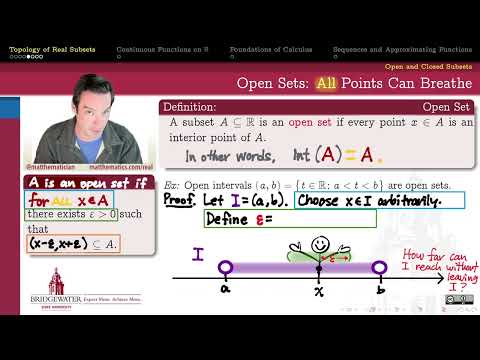
Here I give a taste of topology by defining the notion of an open set, give examples, and show its main properties. I further define the notion of an interior. Enjoy this little topology and analysis extravaganza. More videos can be found on my playlist below.

[MathAdam]

Dr. P always starts with "Thanks for watching" and I wonder: How does he KNOW???? Freaky!

[mathwithjanine]

Such a treat to get a taste of topology on Thanksgiving day! :D Happy Thanksgiving!!

[GregBakker]

Really enjoyed this one, thanks for your very clear explanation of these foundations.

[raycao]

Thanks so much for clear graph explanation ! Really makes such abstract topic comes into sense !

[rafaelsarabia]

Thank you so much for this video. It is clear in every detail. Great way to introduce topology.

[hilario-H]

I wish I had seen this video earlier. Good job, doc!

[emanuelvendramini]

Oh yeah, now, we have a taste of powe... topology

[iabervon]

I had to think a bunch about what happens with metric spaces where there's a lower bound on non-zero distances from some points, or, more generally, where there are distances that don't occur. I think you get open balls that are the same as closed balls and individual points being open, which is weird but doesn't cause any problems.

[HarpreetSingh-kezk]

Thank you, Dr., for opening the closed notations on the part of the topology (open sets).

Is the Borel sigma-algebra also related to proof 3 at 16:10?

Kindly acknowledge.

[DrWeselcouch]

A TASTE of Topology on Thanksgiving. I see what you did there!

[FT]

6:33 this could be fleshed out using triangle inequality!

[rishabhbhutani]

Hmm this is really interesting. One can clearly see that the proof of 3 for a finite intersection of open sets is not valid for infinite amount of intersections. 18:21 . This is because there would be a infinite amount of r's (r1, r2, ...) so instead of a "min" one must use a "inf". Of course, an infimum of a set of positive real numbers can be zero so the proof is not valid because you are using a strict inequality. However, simply saying that a proof does not work for a specific statement is not a proof in its own right. For this, you can consider the counterexample which you gave at around 11:13. Hopefully whatever I said made sense. Thank you Dr. P for the clear explanations as always.

[Stellectis]

Okay, I'm not this good at math but I'm going to give this a try. If x is an element of (a, b) and I want to know if I have an open set. Then I define the limits first of (a, b) say, a=1, b=100, x1=10, can I lead myself to believe that A≤x≤B is defining an open set, and A<x>B or A>x<B is closed?

[willdurie]

No context opening this at 0:55 is a riot

[NH-zhmp]

Hello Dr Peyam, may you make a clip about Einstein's general theory of relativity in mathematic ? That will be very nice, thank you so much.

[imrematajz]

At 11:50 you said logically that the intersection of the infinitely many open sets reduce to the zero set, which is closed. At the same time at the beginning at 9:30 you claimed without proof (axiom?) that the Empty set denoted as Zero and S are open. I am confused at this point...can you please help me see where my confusion comes from and how it can be remedied?

[Pestrutsi]

Concerning the ending Ex2: Doesn't Q have nothing but interior points if you consider with it a topology defined only within rational numbers? I mean if you consider Q with the topology induced by the Euclidean metric of the reals, as I take was done here, then surely Q will have no interior points, it all depends on which topology you choose to use.

[aneeshsrinivas]

Are there any good theorems about when a closed set is indeed not open?

[stevethecatcouch]

The points at most r away from x is a closed ball. The open ball around x is the points less than r away from x. Your symbolic statements were all correct. Your verbal ones were flawed.

[lemniscatepower]

The thing i understood is that boundary point in open sets are not achieved that' s why the small ball can't cross the subset without breaking continuity ... ball is not defined on boundary of subset that why its open subsets ... am i in right track or not if not please tell me where do i wrong