filmov
tv
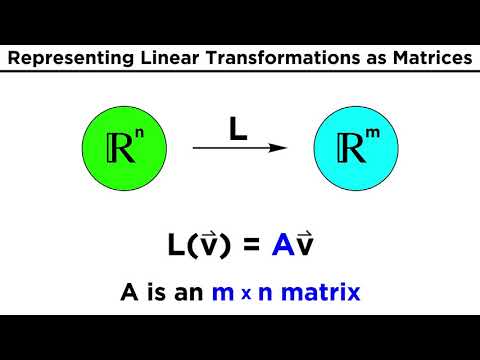
Linear Transformation

Показать описание
. . Let T₁ and T₂ be linear operators on R² defined by \Gamma_{1}(x,y)=(y,x) and T_{2}(x,y)=(x,0)
Compute T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2}T_{2} As~L(R^{\angle}) R2 is a vector space, which is closed under addion and scalar
A\rightarrow(B
Sol multiplication
T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2} {}^{2},{T_{2}}^{2} 1. (T_{1}+T_{2})(x,y) = T (x, y) + T₂ (x, y) for (x, y) ER² =(y,x)+(x,0) = (y+x, x+0) =(x+y,x)
09(B)
xy ∈ Reals [y+x=x+y」
2. (T₂ T₁) (x, y) = T2 [T₁ (x, y)] =T_{2}[y,x] =(y, 0)
3. (T₁ T2) (x, y) =T_{1}[T_{2}(x,y)] =T_{1}[x,0] =(0,x)
4. ({T_{1}}^{2})(x,y)=T_{1}[T_{1}(x,y)] =T_{1}(y,x) =(x,y)=I[(x,y)] T_{1}^{2}=I where I is an identity operator
[by def. of T₁]
[by def, of T2]
[by def. of T
C.
[by def. of T
5. ({T_{2}}^{2})(x,y)=T_{2}[T_{2}(x,y)] =T_{2}[x,0] =(x,0).=T_{2}(x,y)
f\cdot{T_{2}}^{2}
ample 4. (a) Let T_{1}:R^{3}\rightarrow R^{2}; and T_{2}:R^{3}\rightarrow R^{2} be two
Compute T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2}T_{2} As~L(R^{\angle}) R2 is a vector space, which is closed under addion and scalar
A\rightarrow(B
Sol multiplication
T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2} {}^{2},{T_{2}}^{2} 1. (T_{1}+T_{2})(x,y) = T (x, y) + T₂ (x, y) for (x, y) ER² =(y,x)+(x,0) = (y+x, x+0) =(x+y,x)
09(B)
xy ∈ Reals [y+x=x+y」
2. (T₂ T₁) (x, y) = T2 [T₁ (x, y)] =T_{2}[y,x] =(y, 0)
3. (T₁ T2) (x, y) =T_{1}[T_{2}(x,y)] =T_{1}[x,0] =(0,x)
4. ({T_{1}}^{2})(x,y)=T_{1}[T_{1}(x,y)] =T_{1}(y,x) =(x,y)=I[(x,y)] T_{1}^{2}=I where I is an identity operator
[by def. of T₁]
[by def, of T2]
[by def. of T
C.
[by def. of T
5. ({T_{2}}^{2})(x,y)=T_{2}[T_{2}(x,y)] =T_{2}[x,0] =(x,0).=T_{2}(x,y)
f\cdot{T_{2}}^{2}
ample 4. (a) Let T_{1}:R^{3}\rightarrow R^{2}; and T_{2}:R^{3}\rightarrow R^{2} be two
Compute T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2}T_{2} As~L(R^{\angle}) R2 is a vector space, which is closed under addion and scalar
A\rightarrow(B
Sol multiplication
T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2} {}^{2},{T_{2}}^{2} 1. (T_{1}+T_{2})(x,y) = T (x, y) + T₂ (x, y) for (x, y) ER² =(y,x)+(x,0) = (y+x, x+0) =(x+y,x)
09(B)
xy ∈ Reals [y+x=x+y」
2. (T₂ T₁) (x, y) = T2 [T₁ (x, y)] =T_{2}[y,x] =(y, 0)
3. (T₁ T2) (x, y) =T_{1}[T_{2}(x,y)] =T_{1}[x,0] =(0,x)
4. ({T_{1}}^{2})(x,y)=T_{1}[T_{1}(x,y)] =T_{1}(y,x) =(x,y)=I[(x,y)] T_{1}^{2}=I where I is an identity operator
[by def. of T₁]
[by def, of T2]
[by def. of T
C.
[by def. of T
5. ({T_{2}}^{2})(x,y)=T_{2}[T_{2}(x,y)] =T_{2}[x,0] =(x,0).=T_{2}(x,y)
f\cdot{T_{2}}^{2}
ample 4. (a) Let T_{1}:R^{3}\rightarrow R^{2}; and T_{2}:R^{3}\rightarrow R^{2} be two
Compute T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2}T_{2} As~L(R^{\angle}) R2 is a vector space, which is closed under addion and scalar
A\rightarrow(B
Sol multiplication
T_{1}+T_{2},T_{2}T_{1},T_{1}T_{2},{T_{1}}^{2} {}^{2},{T_{2}}^{2} 1. (T_{1}+T_{2})(x,y) = T (x, y) + T₂ (x, y) for (x, y) ER² =(y,x)+(x,0) = (y+x, x+0) =(x+y,x)
09(B)
xy ∈ Reals [y+x=x+y」
2. (T₂ T₁) (x, y) = T2 [T₁ (x, y)] =T_{2}[y,x] =(y, 0)
3. (T₁ T2) (x, y) =T_{1}[T_{2}(x,y)] =T_{1}[x,0] =(0,x)
4. ({T_{1}}^{2})(x,y)=T_{1}[T_{1}(x,y)] =T_{1}(y,x) =(x,y)=I[(x,y)] T_{1}^{2}=I where I is an identity operator
[by def. of T₁]
[by def, of T2]
[by def. of T
C.
[by def. of T
5. ({T_{2}}^{2})(x,y)=T_{2}[T_{2}(x,y)] =T_{2}[x,0] =(x,0).=T_{2}(x,y)
f\cdot{T_{2}}^{2}
ample 4. (a) Let T_{1}:R^{3}\rightarrow R^{2}; and T_{2}:R^{3}\rightarrow R^{2} be two
 0:10:59
0:10:59
 0:13:52
0:13:52
 0:09:11
0:09:11
 0:10:47
0:10:47
 0:11:32
0:11:32
 0:09:06
0:09:06
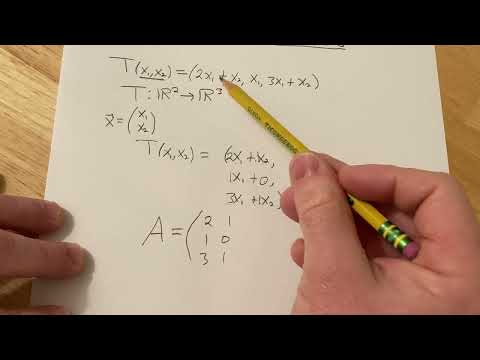 0:05:19
0:05:19
 0:08:28
0:08:28
 0:58:50
0:58:50
 0:09:23
0:09:23
 0:16:01
0:16:01
 0:11:22
0:11:22
 0:04:46
0:04:46
 0:32:58
0:32:58
 0:14:00
0:14:00
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:19:53
0:19:53
 0:24:13
0:24:13
 0:27:35
0:27:35
 0:10:04
0:10:04
 0:09:19
0:09:19
 0:04:09
0:04:09
 0:13:49
0:13:49
 0:13:10
0:13:10