filmov
tv
Help.. find the least k so the given quadratic equation has real solutions Reddit A-level maths
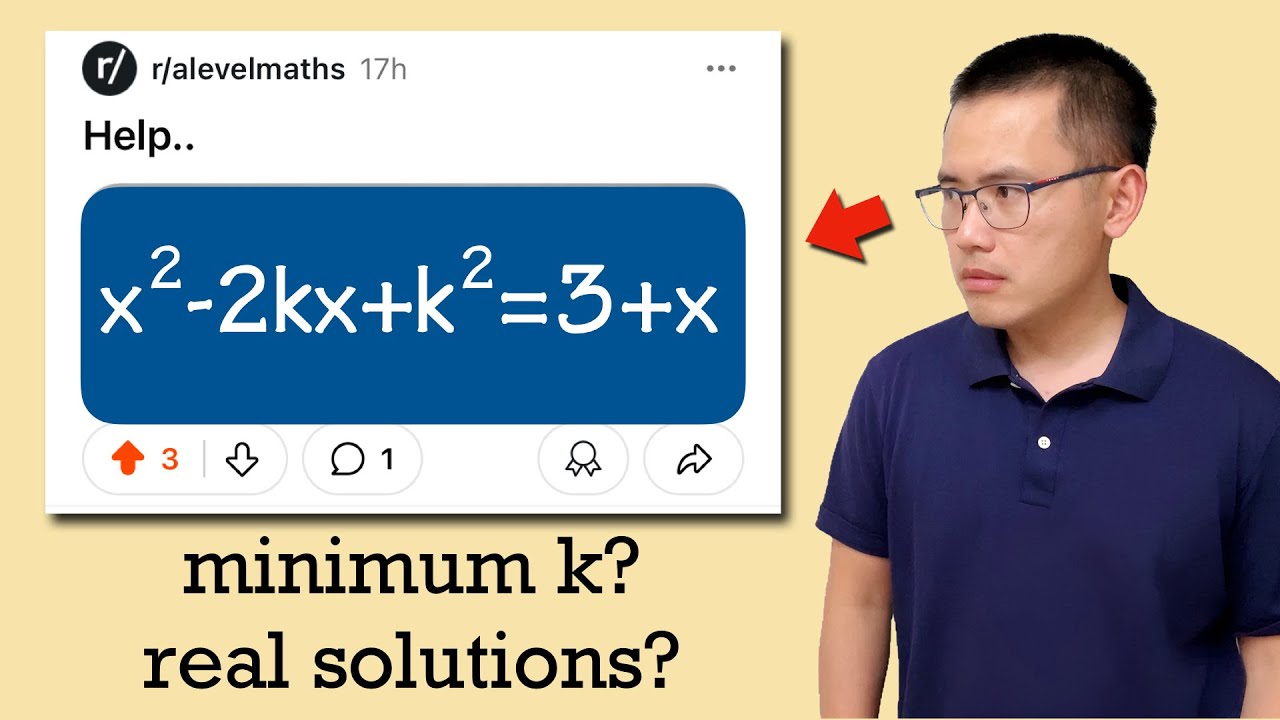
Показать описание
We are given x^2-2kx+k^2=3+x and have to find the least value of k so the quadratic equation has real solutions. This is a typical A-level maths problem that requires you to know about quadratic equations and discrimination. Subscribe to @bprpmathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Help.. find the least k so the given quadratic equation has real solutions Reddit A-level maths
class 10th Pyq How to Find the Least Positive Value of k for Rational Roots in a Quadratic Equation
Longest subsequence where each character occurs at least k times | GeeksforGeeks
Find the least positive value of k for which the equation x^2+kx+4=0 has real roots...|| RD Class 10
Find the least positive value of `k` for which the equation `x^2+k x+4=0` has real roots.
Longest Substring with At Least K Repeating Characters - LeetCode Problem 395
Count Subarrays Where Max Element Appears at Least K Times - Leetcode 2962 - Python
Leetcode 3097: Shortest Subarray With OR at Least K II
Longest Substring with At Least K Repeating Characters | Live Coding with Explanation | Leetcode#395
Code Review: Given n numbers, find out the least k numbers from them (4 Solutions!!)
Leetcode 2962: Count Subarrays Where Max Element Appears at Least K Times
Find the least positive value of k forhich the equation x^2+k x+4=0 has real roots. W
Worst ways people have died😰 #shorts
395. Longest Substring with At Least K Repeating Characters - Day 26/30 Leetcode November Challenge
Find the least positive value of k if x²+kx+k=0 has real roots | the least positive value of k for
Longest Substring with At Least K Repeating Characters | Leetcode 395 | Nov2020 Day 26 Challeneg
Shortest Subarray with Sum at Least K | Leetcode #862
Longest Substring with At Least K Repeating Characters | LeetCode 395 | C++, Java, Python
8.0 Longest Substring with At Least K Repeating Characters | Divide and Conquer - full explanation
Longest Substring with At Least K Repeating Characters | Sliding Window Technique | HashMap | Java
How to Find the LCM using Prime Factorization | Least Common Multiple | Math with Mr. J
IIT JEE APPLICATION OF DERIVATIVES Find the least value of `k` for which the function `x^2+k x+1...
Find the least value of K for which 7864K3 is divisible by 7.
3097. Shortest Subarray With OR at Least K II | Sliding Window | 2 Pointers | Bit Manipulation
Комментарии
 0:04:19
0:04:19
 0:02:15
0:02:15
 0:02:13
0:02:13
 0:02:23
0:02:23
 0:01:31
0:01:31
 0:13:37
0:13:37
 0:14:57
0:14:57
 0:19:34
0:19:34
 0:05:31
0:05:31
 0:05:58
0:05:58
 0:13:30
0:13:30
 0:03:33
0:03:33
 0:00:20
0:00:20
 0:21:22
0:21:22
 0:04:35
0:04:35
 0:08:42
0:08:42
 0:21:31
0:21:31
 0:21:05
0:21:05
 0:23:32
0:23:32
 0:45:46
0:45:46
 0:07:53
0:07:53
 0:01:10
0:01:10
 0:01:21
0:01:21
 0:28:58
0:28:58