filmov
tv
integral of 1/(sin(x)+cos(x))^2, calculus 2 integrals

Показать описание
angle additional formula: a*sin(x)+b*cos(x)=Acos(x+𝛼)
blackpenredpen,
math for fun
blackpenredpen,
math for fun
integral of 1/(sin(x)+cos(x))^2, calculus 2 integrals
Integration 22 : Integration of 1/ (3+ 2 sin x + cos x) || JBR Online classes
Integral of (1 - sin(x))/cos(x)
weierstrass substitution, integral of 1/(1+sin(x)+cos(x))
Integral of 1/(sin(x)+cos(x))
Integration By Trigonometric Functions Problem#2.∫ dx/(sinx cosx)
trig integrals involving sine and cosine (calculus 2)
How REAL Men Integrate Functions
GCE O level Additional Mathematics (4047) Year 2024 Paper 1 | TYS Past Year Paper Full Solution!
integration by parts is easy
Integral of 1/sin^2(x)+cos^2(x)
Integral of 1/(sin^2(x)cos^2(x))
Integral of sin x(cos x + 1) ❖ Calculus 1 ❖ U-Substitution ❖ Trig Integral
Evaluate the integral : ∫ (1 + 2sinx)/cos²x dx
1/sinx+cosx integral |Integration isc |Integral class12 |Integration #integral #maths #integralmaths
Integration by Partial Fractions, Integral of 1/sin² x cos x, Calculus 2
Calculus: Indefinite Integration- Integral of 1/(1 + Sin x + Cos x)
Integral of 1 / [ (sin x)^6 + (cos x)^6 ] from 0 to pi/2
Arc Length Example: y = 2(x+1)sin(x)cos(x) over [-2,2]
Integral of sin x/(1+cos x)^2 ❖ Calculus 1 ❖ U-Substitution ❖ Trig Integrals
Integral of sin(x/2) cos(x/2) ❖ Calculus
Integral 1/sin x
The Derivative You Didn't See Coming: sinx w.r.t cos𝑥cosx!#maths
Integral of cos x/(1 + sin^2 x) ❖ Calculus 1 ❖ Trig Integrals
Комментарии
 0:07:18
0:07:18
 0:03:19
0:03:19
 0:05:23
0:05:23
 0:02:34
0:02:34
 0:10:06
0:10:06
 0:05:25
0:05:25
 0:15:42
0:15:42
 0:00:35
0:00:35
 0:51:41
0:51:41
 0:00:33
0:00:33
 0:00:13
0:00:13
 0:03:01
0:03:01
 0:02:50
0:02:50
 0:03:47
0:03:47
 0:00:27
0:00:27
 0:06:48
0:06:48
 0:03:53
0:03:53
 0:03:55
0:03:55
 0:00:31
0:00:31
 0:03:23
0:03:23
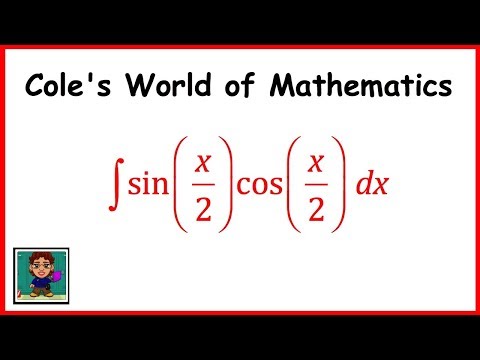 0:03:38
0:03:38
 0:00:37
0:00:37
 0:00:33
0:00:33
 0:02:12
0:02:12