Find kth bit in nth binary string leetcode 1545 python

okay, let's dive deep into the leetcode problem "1545. find kth bit in nth binary string" and craft a detailed tutorial with a python solution, explanation, and optimization considerations.

**problem statement**

the problem defines a sequence `sn` of binary strings as follows:

* `s1 = "0"`
* `sn = sn-1 + "1" + invert(reverse(sn-1))` for `n 1`

here:

* `+` denotes string concatenation.
* `invert(s)` inverts all bits in the string `s` (0 becomes 1, and 1 becomes 0).
* `reverse(s)` reverses the string `s`.

given two positive integers `n` and `k`, find the `k`th bit (1-indexed) in the string `sn`.

**example**

**understanding the problem and approach**

the key to solving this problem efficiently lies in understanding the recursive nature of the string construction. directly constructing the string `sn` can lead to significant memory usage and performance issues, especially for large values of `n`. instead, we will exploit the structure of the string to determine the `k`th bit *without* explicitly building the entire string.

here's the core idea:

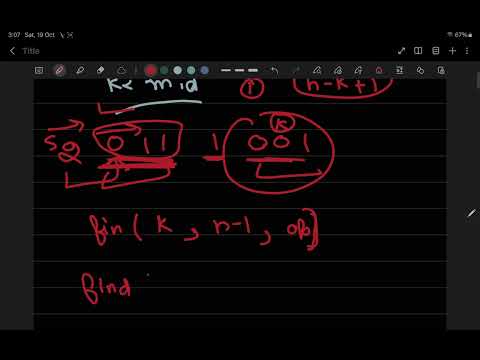
1. **binary search approach:** we can use a binary search-like approach to find the `k`th bit. the length of `sn` is given by `len(sn) = 2^n - 1`. we can determine if the `k`th bit lies in the left half (sn-1), the middle '1', or the right half (inverted and reversed sn-1).

2. **recursion with logic:** recursively work our way down to `s1 = "0"`. each step will either:

* find the bit directly (when `n` is 1).
* determine the side (`sn-1` or its inverted/reversed counterpart) where the `k`th bit resides.
* update `k` and potentially "invert" the result based on the position and inversion.

**python implementation**

**explanation of the code**

1. **base case:** `if n == 1: return "0"`
* this is our stopping condition. `s1` is simply "0".

2. **calculate length and middle:**
* `length = (1 n) - 1`: calculates the length of the string `sn`. `1 n` is equival ...

#LeetCode #Python #windows
kth bit
nth binary string
LeetCode
binary representation
bit manipulation
Python
string indexing
binary strings
algorithm
recursive approach
bitwise operations
search algorithm
find kth bit
complexity analysis
coding challenge