LPP Graphical Method - 4 Negative sign in constraints and objective function

Показать описание

#OperationsResearch #Math #Statistics #Linear Programming #GraphicalMethod #Constraint #Maximization #Inequality #ObjectiveFunction #FreeLecture #FreeStudy #Solution

LPP - Graphical Method

Case - LPP with "less than" sign and Negative sign in constraints

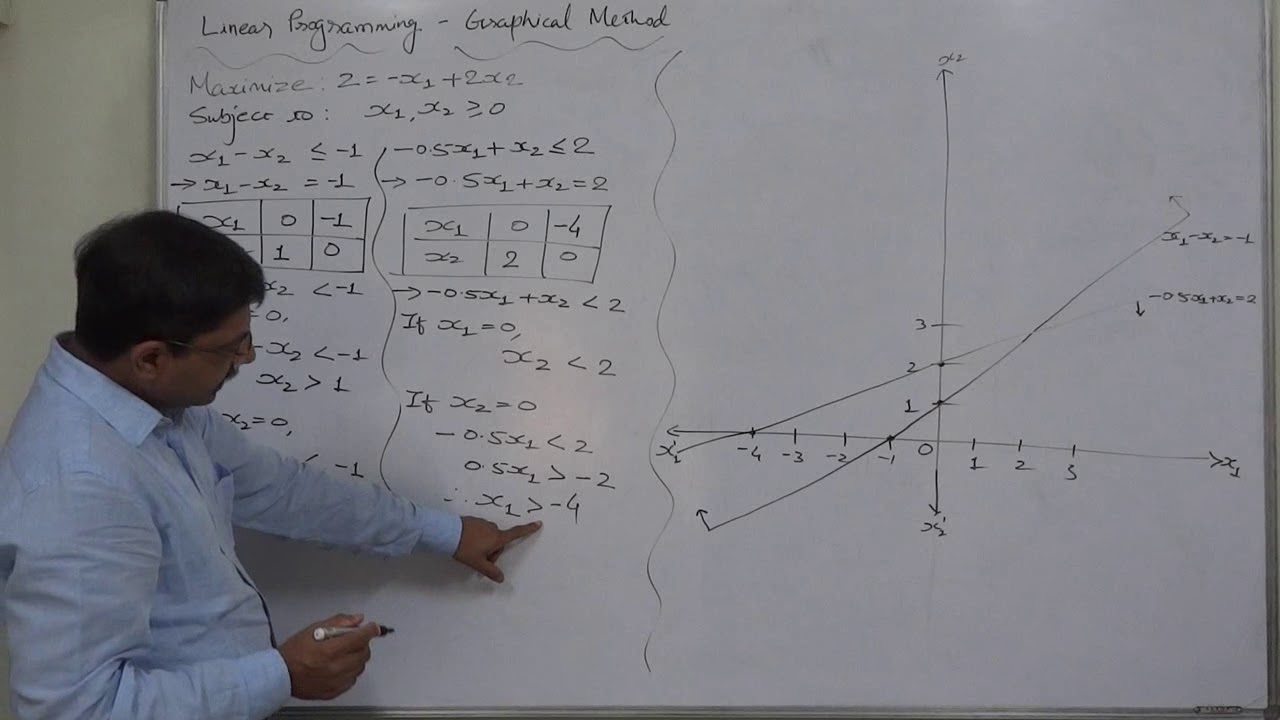
Solve the following LPP through the Graphical Method:
Maximize: Z = -X1 + 2X2
Subject to -

X1 - X2 ≤ -1
0.5X1 + X2 ≤ 2
X1 and X2 ≥ 0

If there are two variables in an LP problem, it can be solved by graphical method. Let the two variables be x1 and x2. The variable x1 is represented on x-axis and x2 on y-axis. Due to non-negativity condition, the variables x1 and x2 can assume positive values and hence if at all the solution exists for the problem, it lies in the first quadrant. The steps used in graphical method are summarized as follows:
Step 1: Replace the inequality sign in each constraint by an equal to sign.

Step 2: Represent the first constraint equation by a straight line on the graph. Any point on this line satisfies the first constraint equation. If the constraint inequality is ‘less than’ type, then the area (region) below this line satisfies this constraint. If the constraint inequality is of ‘greater than’ type, then the area (region) above the line satisfies this constraint.

Step 3: Repeat step 2 for all given constraints.

Step 4: Shade the common portion of the graph that satisfies all the constraints simultaneously drawn so far. This shaded area is called the ‘feasible region’ (or solution space) of the given LP problem. Any point inside this region is called feasible solution and provides values of x1 and x2 that satisfy all constraints.

Step 5: Find the optimal solution for the given LP problem. The optimal solution may be determined using the Extreme Point method. In this method, the coordinates of each extreme point are substituted in the objective function equation; whichever solution has optimum value of Z (maximum or minimum) is the optimal solution.

OR, Operations Research, Math, Mathematics, Linear Programming, LPP, Graphical Method, Constraints, Inequality, Equality, Equation, MBA, MCA, CA, CS, CWA, CMA, CPA, CFA, BBA, BCom, MCom, BTech, MTech, CAIIB, FIII, Graduation, Post Graduation, BSc, MSc, BA, MA, BE, Diploma, Production, Finance, Management, Commerce, Engineering, Grade-11, Grade- 12