filmov
tv
Proof of the Multivariable Chain Rule
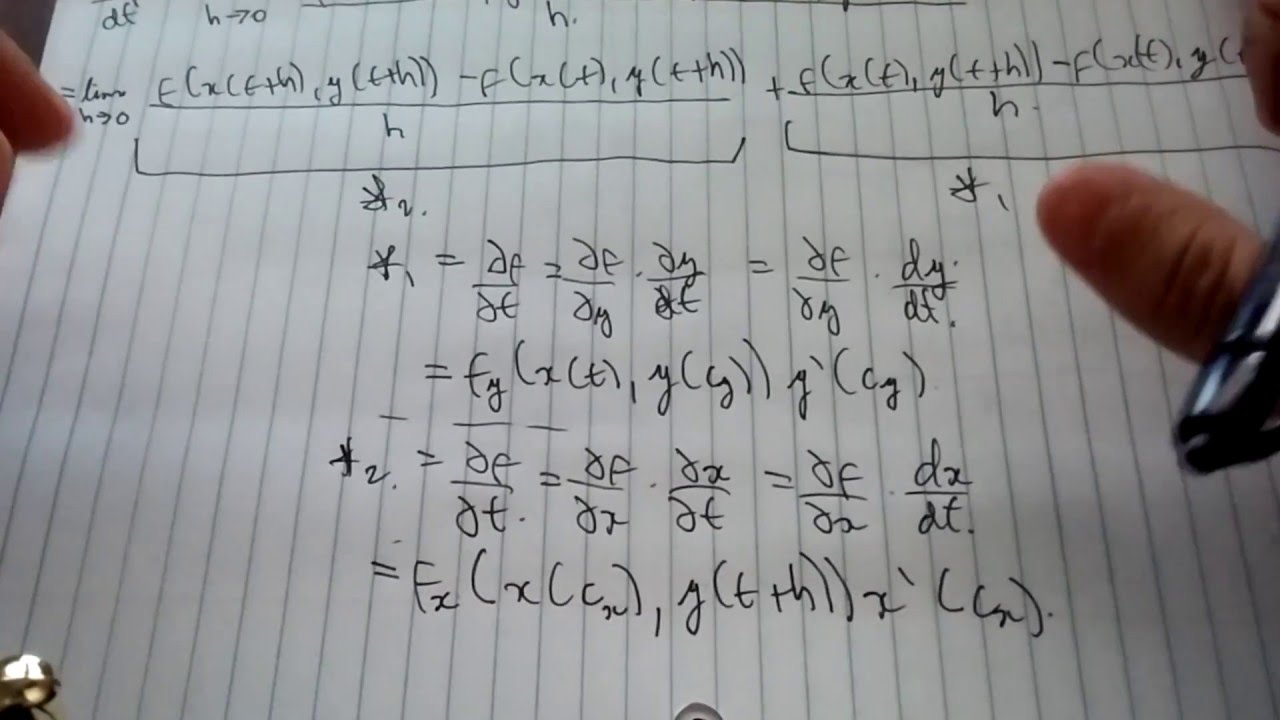
Показать описание
Proof of the Multivariable Chain Rule
Multivariable Chain Rule Proof
Multivariable chain rule intuition
Proof of multivariable chain rule
The Multi-Variable Chain Rule: Derivatives of Compositions
Multivariable chain rule
Multivariable chain rule proof
Find multivariable chain rule from dependence diagram in under one minute
What Is The Multivariable Chain Rule And Why Does It Work?
Multivariable Chain Rule: Proof
Multivariable Chain Rule Example With Partial Derivative
Multivariable chain rule | Lecture 14 | Vector Calculus for Engineers
Proof of Chain Rule for Multivariable Functions (Vector Valued)
Chain rule proof | Derivative rules | AP Calculus AB | Khan Academy
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus
Multivariable Calculus: Chain Rule for Multivariable Functions
Proof of a chain rule for partial derivatives
Concise Modular Calculus [82/97]: The Multivariable Chain Rule
Difference Between Partial and Total Derivative
Multivariable Calculus | The chain rule.
Chain Rule With Partial Derivatives - Multivariable Calculus
Calculus 3 Lecture 13.5: The Chain Rule for Multivariable Functions
Multivariable chain rule and differentiability
The Multivariable Chain Rule
Комментарии
 0:09:32
0:09:32
 0:28:50
0:28:50
 0:07:47
0:07:47
 0:09:01
0:09:01
 0:10:47
0:10:47
 0:09:33
0:09:33
 0:06:55
0:06:55
 0:00:49
0:00:49
 0:06:44
0:06:44
 0:33:12
0:33:12
 0:03:41
0:03:41
 0:09:19
0:09:19
 0:25:55
0:25:55
 0:05:39
0:05:39
 0:15:56
0:15:56
 0:37:02
0:37:02
 0:11:06
0:11:06
 0:44:07
0:44:07
 0:01:44
0:01:44
 0:11:29
0:11:29
 0:21:10
0:21:10
 2:11:52
2:11:52
 0:48:54
0:48:54
 0:14:42
0:14:42