filmov
tv
Improper integral with two infinite bounds | AP Calculus BC | Khan Academy

Показать описание
Infinite both ways! Created by Sal Khan.
AP Calculus BC on Khan Academy: Learn AP Calculus BC - everything from AP Calculus AB plus a few extra goodies, such as Taylor series, to prepare you for the AP Test
For free. For everyone. Forever. #YouCanLearnAnything
Improper Integral with Two Infinite Limits
Improper integral with two infinite bounds | AP Calculus BC | Khan Academy
improper integral of x*e^(-x^2) from -inf to +inf
Improper Integrals - Convergence and Divergence - Calculus 2
Improper Integral - TWO Infinite Bounds | Definition and How to Compute it
Improper Integrals of Type II (Discontinuous Integrand) in 12 Minutes
Improper integral with two infinite bounds | AP Calculus BC | Khan Academy Hebrew
Improper integral with two infinite bounds
Improper Integrals of Type I (Infinite Intervals) in 12 Minutes
Improper Integrals with Two Infinite Bounds: Explanation and Examples | Sam's Calculus Tutorial...
Calculus 2 Lecture 7.6: Improper Integrals
Comparison Test for Improper Integrals
Improper Integrals: How to Integrate with Infinities, 2 ways!
Improper integrals with infinite limits - Calculus
Math Integral Calculus - Improper integral with two infinite bounds
Improper Integral with Infinite Interval and Discontinuous Integrand!
Calculus 2 - 11 - Improper Integral
Improper Integrals Two Infinities
Improper Integral with Infinite Discontinuity
Evaluate Improper Integral xe^(-x^2) dx over (-infinity, infinity). Infinite Integration Limits
Evaluating Improper Integrals
Improper integrals discontinuous integrand
The Improper Integral of e^(-x) from 0 to Infinity
Determine whether each integral is convergent or divergent. Integral from 2 to infinity of e^-5p dp
Комментарии
 0:05:57
0:05:57
 0:11:27
0:11:27
 0:05:20
0:05:20
 0:13:56
0:13:56
 0:10:02
0:10:02
 0:11:23
0:11:23
 0:11:27
0:11:27
 0:11:27
0:11:27
 0:11:59
0:11:59
 0:16:25
0:16:25
 2:48:31
2:48:31
 0:07:55
0:07:55
 0:08:51
0:08:51
 0:25:14
0:25:14
 0:11:27
0:11:27
 0:02:58
0:02:58
 0:02:49
0:02:49
 0:08:10
0:08:10
 0:08:40
0:08:40
 0:05:45
0:05:45
 0:12:24
0:12:24
 0:21:19
0:21:19
 0:03:28
0:03:28
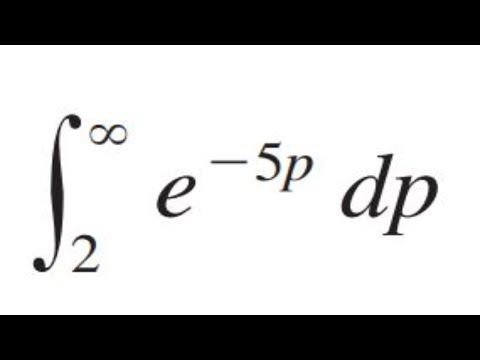 0:04:27
0:04:27