filmov
tv
Estimating The Error In Fit Parameters

Показать описание
This is a very quick introduction to finding the error in fit parameters as well as the propagation of error in measurement to the error in calculated results.
Estimating The Error In Fit Parameters
Line of Best Fit Equation
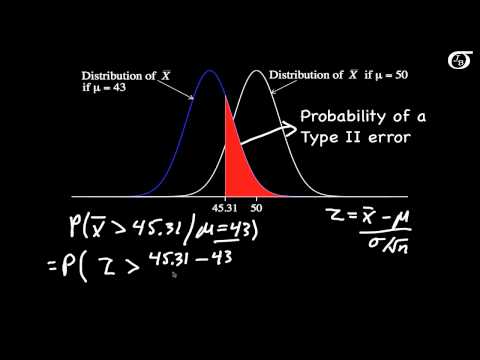
Calculating Power and the Probability of a Type II Error (A One-Tailed Example)
Maximum Likelihood, clearly explained!!!
Linear Regression Using Least Squares Method - Line of Best Fit Equation
How to fit a straight line to data in Excel, and estimate the uncertainty in the gradient
Estimating the line of best fit exercise | Regression | Probability and Statistics | Khan Academy
Calculating the slope of a best fit line
Linear regression full course tutorials part 14
Estimating a Line of Best Fit (technology approach)
Estimating slope of line of best fit : Khan Academy
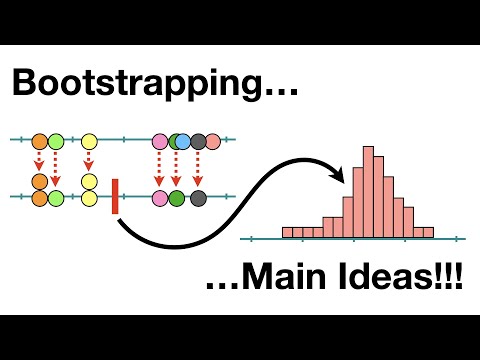
Bootstrapping Main Ideas!!!
Introduction to residuals and least squares regression
Population and Estimated Parameters, Clearly Explained!!!
How To... Perform Simple Linear Regression by Hand
Type 1 errors | Inferential statistics | Probability and Statistics | Khan Academy
DEMO: Estimation of SEM and the Analysis of Fit - Concepts, Interpretation, and Common Pitfalls
Correlation Coefficient
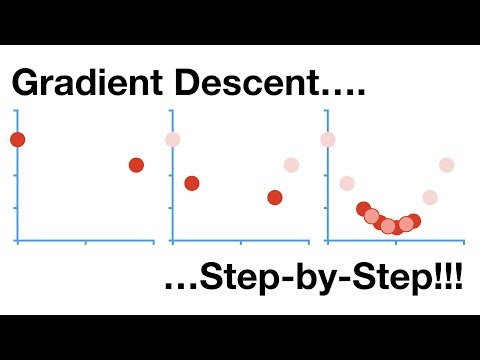
Gradient Descent, Step-by-Step
Introduction to Type I and Type II errors | AP Statistics | Khan Academy
Squared error of regression line | Regression | Probability and Statistics | Khan Academy
Line of Best Fit: Finding the Equation and Calculating Residual
Estimating the line of best fit exercise
Linear mixed effects models
Комментарии
 0:16:07
0:16:07
 0:04:00
0:04:00
 0:11:32
0:11:32
 0:06:12
0:06:12
 0:15:05
0:15:05
 0:07:52
0:07:52
 0:01:17
0:01:17
 0:07:15
0:07:15
 8:17:43
8:17:43
 0:10:16
0:10:16
 0:15:46
0:15:46
 0:09:27
0:09:27
 0:07:39
0:07:39
 0:14:31
0:14:31
 0:10:55
0:10:55
 0:03:24
0:03:24
 1:00:59
1:00:59
 0:12:57
0:12:57
 0:23:54
0:23:54
 0:05:03
0:05:03
 0:06:47
0:06:47
 0:04:59
0:04:59
 0:01:17
0:01:17
 0:18:37
0:18:37