filmov
tv
Open, closed, both and neither sets
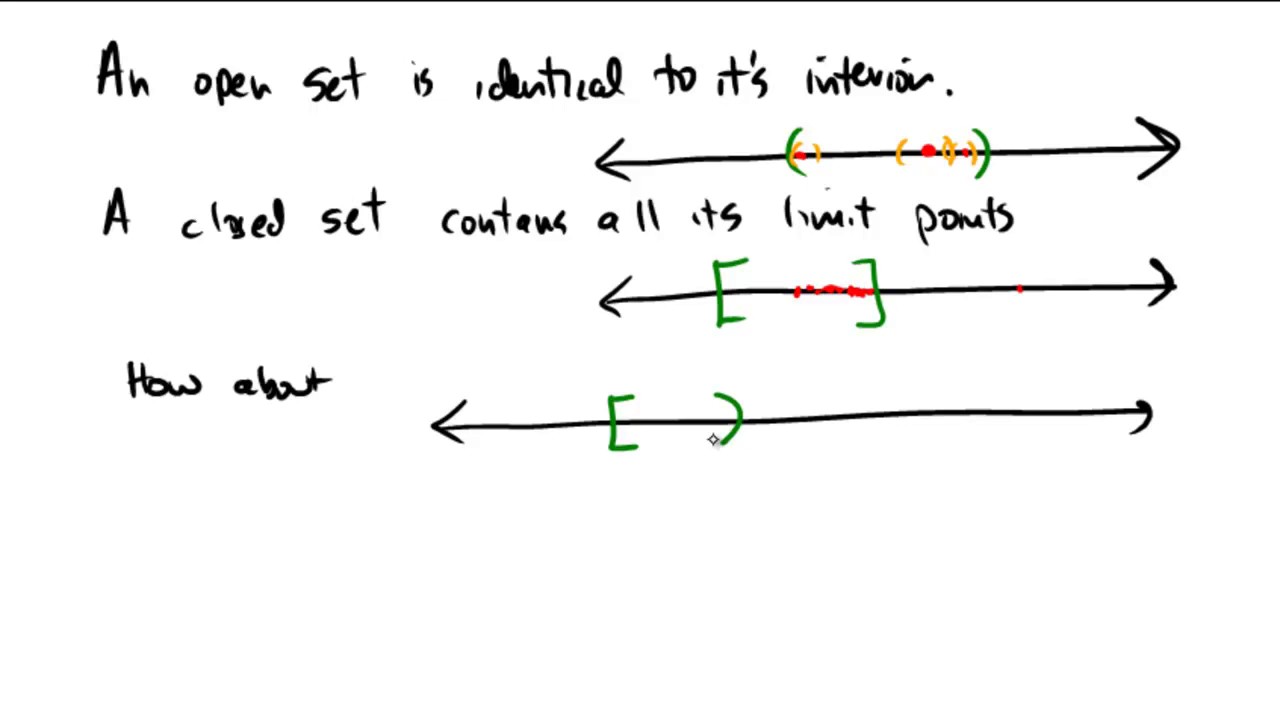
Показать описание
This video briefly explores (in R) sets that are open, closed, neither and both (clopen)
Open, closed, both and neither sets
An example of neither open nor closed set (6 Solutions!!)
Examples of open, closed and neither open nor closed regions in space
#Example of neither open set nor closed set, solution of S.K.Mapa, set inR
#Example of Neither open set nor closed set, Solution of S.K.Mapa book, set in R
Open, Closed, and Isolated Systems Explained | Class 11 Physics | Thermodynamics
The set Q of all rational numbers is neither a closed subset of R nor an open subset of R
Interval Notation - Open Intervals, Closed Intervals, and Neither
Piecewise Functions - Limits and Continuity | Calculus
Either Vs. Neither and Other Grammar Concepts
BOTH.. AND/NOT ONLY.. BUT ALSO/NEITHER.. NOR/EITHER... OR/WHETHER... OR
Quantifiers - 'Both', 'Either' and 'Neither'
The law of conservation of mass - Todd Ramsey
How to say 'Me too/Me neither' in French | By Suchita| For classes - +91-8920060461
Recursive Formulas For Sequences
Symmetry EVEN ODD NEITHER
THE CONDITIONALS - 0,1,2 & 3 Conditionals& QUIZ - English Grammar Lesson (+ Free PDF & Q...
We have no moat, neither does OpenAI
A French Port And A Ferry Home. And Why Neither Was As Expected! Brittany Ferries Cherbourg To Poole
Neither opened nor closed doors indicates the will of God for your life
The Big Misconception About Electricity
Worlds most closed neither
Google: 'We have no moat, and neither does Open AI'
Correlative Conjunctions: 'both...and', 'either...or', and 'neither...nor&a...
Комментарии
 0:05:14
0:05:14
 0:03:02
0:03:02
 0:08:53
0:08:53
 0:14:44
0:14:44
 0:16:23
0:16:23
 0:00:58
0:00:58
 0:13:36
0:13:36
 0:08:21
0:08:21
 0:10:06
0:10:06
 0:48:41
0:48:41
 0:12:18
0:12:18
 0:55:41
0:55:41
 0:04:37
0:04:37
 0:00:22
0:00:22
 0:02:54
0:02:54
 0:13:05
0:13:05
 0:10:58
0:10:58
 0:00:54
0:00:54
 0:30:47
0:30:47
 0:11:55
0:11:55
 0:14:48
0:14:48
 0:00:15
0:00:15
 0:15:30
0:15:30
 0:05:36
0:05:36