filmov
tv
please let your students use the DI method for integration by parts
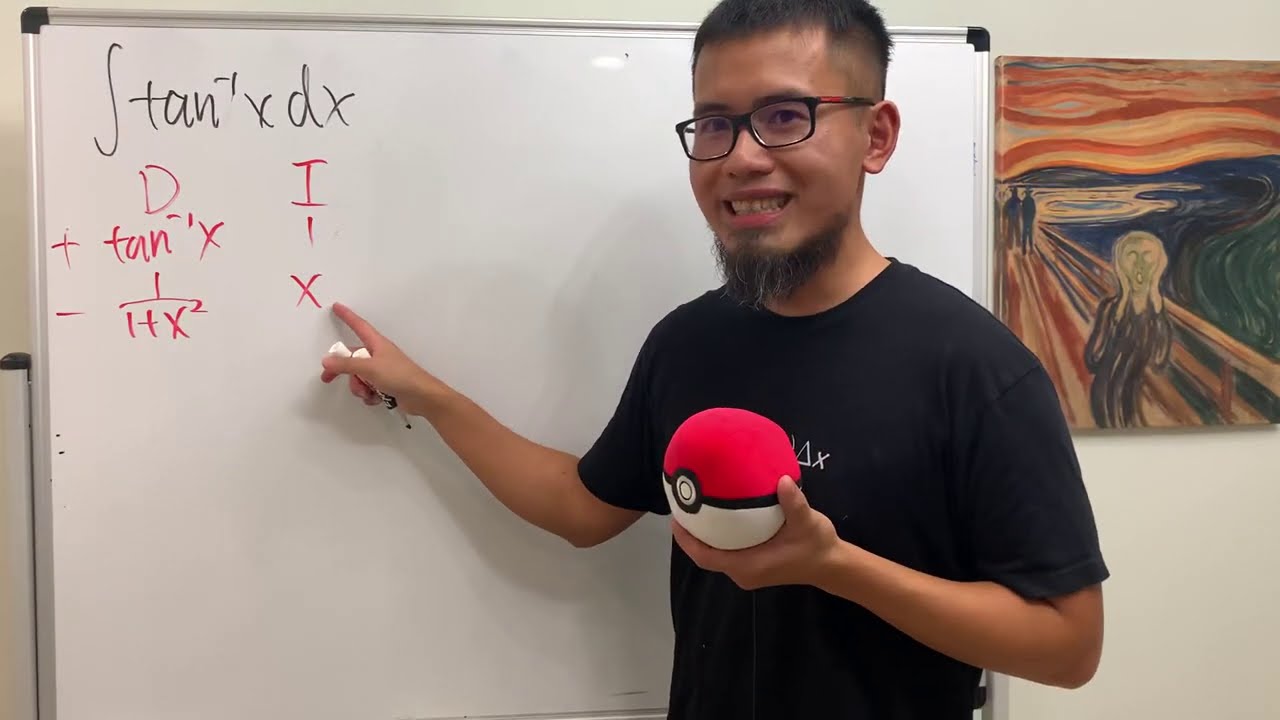
Показать описание
0:00 please let your students use the DI method
0:17 integral of x^2*sin(x) with the DI method
1:20 integral of x^2*sin(x) with the u-dv format
7:11 integral of tan^-1(x)
12:18 integral of e^(-x)*cos(x)
#calculus2 #calculusteacher
please let your students use the DI method for integration by parts
yasui & otoko || i love you so (please let me go.)
Please let me go.. #animation #youtubeshorts #viral #sad #love
The Smiths - Please, Please, Please, Let Me Get What I Want (Official Audio)
Dear Lord, when I get to Heaven, please let me bring my man.
I can’t let go (I just like it) #camailccm #subscribe #gachaedit #gachaclub
This Eminem song will make you cry.. 🥺❤️
Let's just have fun with your loved ones!😎 #PermissiontoDance Challenge only on YouTube #Shorts...
Things on our sailing boat that just make sense ⛵️ #sailing #shorts
Here’s how to make your kids bike sound like a motorcycle. Just flatten a used water bottle .
Just let me use the stack bro please #mtg #magicthegathering #mtgcommunity
Awwwww!!!!you two just make a 'Heart' shape😏😳😇(ft.Aphmau wolf AU)❤💜(short)(Original 💅)...
Earn $900 Just By Listening To Music! (Make Money Online From Home 2023)
Classroom management tools that just make sense in my elementary music class
No Way! Charlie Puth just make a Music out of a Spoon and a Cup
Don't Become An Entrepreneur Just To Make Money
slow cooker pulled chicken | easy recipe to please a crowd or make for meal prep
please let me in your clan 🙏 😊👍 #gaming #roblox #clan
Pt. 2 | These designs didn't make the cut because they just didn't have a strong Why. #ent...
please just let us purge. | The Purge (Transgender) (slowed&reverb)
implementing just one of these habits into your morning routine will make a huge difference
'dear lord, when I get to heaven please let me bring my man' | Twisted Wonderland Gacha |
The Smiths - Please, Please, Please Let Me Get What I Want (Official Lyric Video)
I’m 17, please let me play good riddance # Thank You Kansas City ✨
Комментарии
 0:15:54
0:15:54
 0:00:50
0:00:50
 0:00:23
0:00:23
 0:01:53
0:01:53
 0:00:54
0:00:54
 0:00:17
0:00:17
 0:00:16
0:00:16
 0:00:17
0:00:17
 0:00:42
0:00:42
 0:00:16
0:00:16
 0:00:58
0:00:58
 0:00:24
0:00:24
 0:08:13
0:08:13
 0:00:29
0:00:29
 0:01:00
0:01:00
 0:00:33
0:00:33
 0:00:27
0:00:27
 0:00:12
0:00:12
 0:01:00
0:01:00
 0:00:40
0:00:40
 0:00:27
0:00:27
 0:00:25
0:00:25
 0:01:57
0:01:57
 0:01:01
0:01:01