A Neglected Objection to the Modal Ontological Argument

This video presents an underappreciated approach to resisting modal ontological arguments (MOA). Rather than criticizing the premise that God possibly exists or trying to run a reverse-MOA, in this video I consider the possibility of challenging the modal assumptions which the MOA relies on.

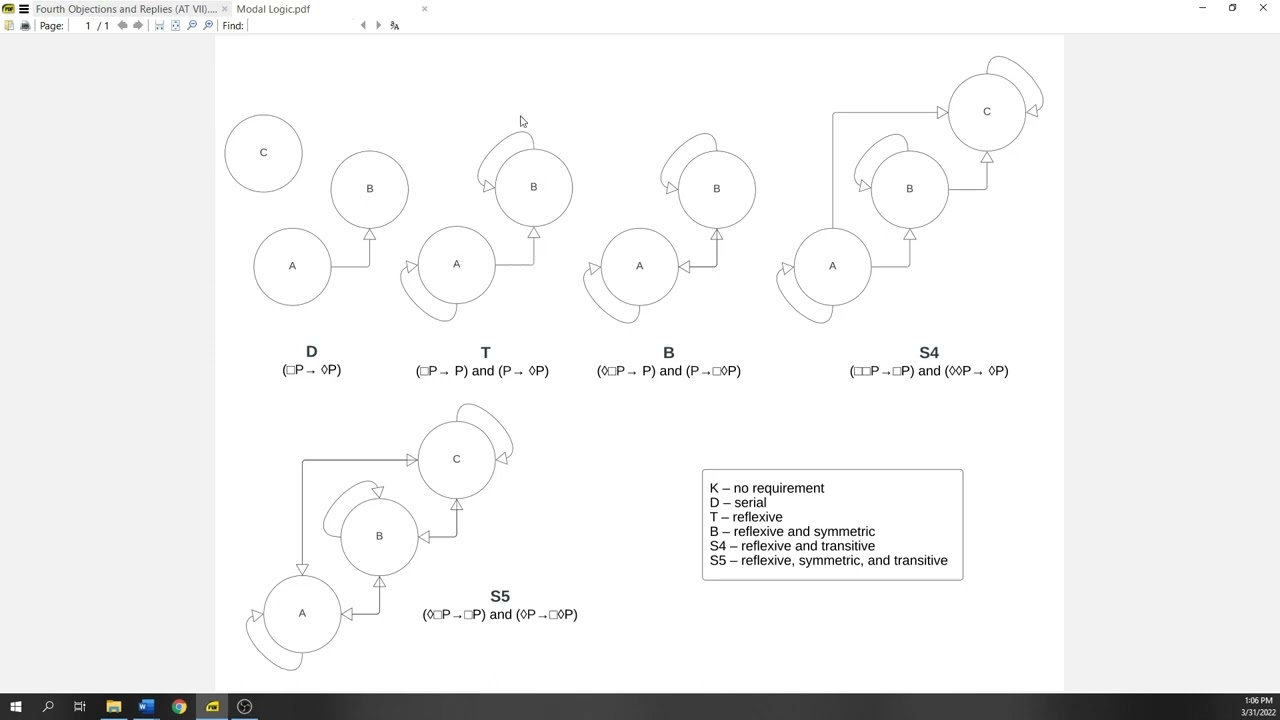
I first lay out the argument. Then I introduce the modal logical terminology and concepts needed to understand why the MOA (in both the weak and the strong forms, as I call them in the video) relies on specific systems of modal logic. Lastly, I present Nathan Salmon's argument against systems S4 and S5, and explain how an argument like that would undermine the MOA.

-----------------------------------------------------------------------------------------------------------------

You can read Plantinga's version of the MOA in his book The Nature of Necessity:

The book I recommend in the video for learning more about modal logic is Ted Sider's Logic for Philosophy:

I also rely on Nathan Salmon's paper "The Logic of What Might Have Been":

And then I mention, as papers that present critiques of the B-system, Dummett's paper "Could There Be Unicorns?" and Kane's "The Modal Ontological Argument":

[michaelcevering]

Hey Joseph -- I'm a PhD candidate at SLU, and a Mormon philosopher. I've been contemplating and working on Mormonism's philosophical relationship to natural theology for the past few years. I'd love to chat more about this. I actually think the MOA isn't so problematic for Mormon philosophy/theology (simpliciter) unless we make particular assumptions that aren't so historically obvious. That being said, I don't attempt apologetics when contemplating proofs, so our approaches *might* differ with regards to Mormonism's relationship to proofs. Anyway, lmk if you'd want to chat sometime.

[ethanf.]

I wonder why he stopped posting? I love his stuff, and I think he's doing something incredibly important that not many other people are doing. Latter Days Saints need to be a part of these broader philosophical discussions (I think we have a lot to say). Hopefully he comes back

[physics_philosophy_faith]

The link to Salmon's paper in the description has a proxy in it, could you replace that with a clean link?

[quad]

What if we take possibility to simply mean a maximally consistent set of propositions?
Then, when we say that from within world A that it's possible we share the same bike as another world, this will be true just in case there is another world wherein 2 of the same bicycle parts as world A are put together (world B).
Then, this proposition would still be true even in world C, since B is still a logically coherent set of propositions, that is coherent even from within C, since the coherency of a world won't differ across worlds. It's either always consistent, or always inconsistent.

It seems to me that you're imposing a further notion of possibility onto S5 than is intended by the designers (a more realist notion I'm actually partial towards, tbh), a version of possibility that's more to do with 'the way that things can go, given the way they currently are', but not the notion of broad logical possibility people like Plantinga may have had in mind. (One where I still think his argument would fail at, since, maximal excellence only entails metaphysical necessity, not broad logical necessity).

[roderictaylor]

Personally, I think transitivity is intuitive, and I wouldn't try to criticize the MOA by criticizing that. Transitivity tells us that if a proposition is necessarily true, then it is necessarily true that it is necessarily true. Would we really want to work in a modality that was not transitive, where there was a proposition P that was necessarily true, but it was possible it was not necessarily true? Equivalently, transitivity says if it it is possible it is possible a proposition is true, then it is possible that proposition is true. Would we really want to work in a modality where there might be a proposition P such that it was both impossible P was true, but it was possible P could be possibly true?

S4 is appropriate for modelling the modality of what in principle can be proven. We can interpret "if a proposition P is necessarily true then it it necessarily true that it is necessarily true" to mean, if we can prove a proposition P must be true, we can prove that we can prove it is true. And that makes sense. If we prove P is true, then we have proven P is true, and we have simultaneously proven that we can prove P is true, by doing it.

In "Set Theory and the Continuum Problem, " mathematicians Smullyan and Melvin Fitting use S4 to help prove the continuum hypothesis cannot be proven true or false using the other standard axioms of set theory. S4 is definitely useful for axiomitizing the modality of provability within mathematics.

My opinion is that Nathan Salmon's argument reveals a genuine difficulty with modal logic, but transitivity is not the problem; rather it is that we have not found a good model of how to talk about cross-world identity.

[roderictaylor]

Thanks for an interesting video that goes much more deeply into models of possible worlds than most other videos. You've given me something to think about. Using only B, we can show that if it is possible that God exists as a necessary being, then it follows God exists, but it does not follow that God exists as a necessary being. I had not understood that before. (I had thought that using symmetry we could show that if it is possible it is necessarily true a MGB then a MGB exists, and then we could then use the definition of a MGB to show it was necessarily true a MGB exists. But I don't think that works now.)

I think the reason this option of rejecting the MOA by criticizing transitivity is neglected might be that even if we grant it, the MOA still shows that if it is possible it is necessarily true God exist, then God exists. If one wishes to even reject that conclusion, one must reject symmetry. But if one rejects symmetry, there is no need to reject transitivity, as the MOA does not work at all in S4.

My own opinion is we do no need to reject S5. Different axiom systems model different modalities. S4 models the modality of what can in principle be known or proven to be necessary. S5 models the modality what is metaphysically necessary, what is in reality necessity regardless of what can be known or proven. The best argument I've seen for using S5 is John P. Burgess's "Which Modal Logic is the Right One."



PS. I used to think that we could use B to show that if it is possible a MGB exists then a MGB exists, and then conclude that from the definition of a MGB that if a MGB exists then it is necessarily true a MGB exists. But after listening to your video, I no longer think that we can use B to show that if it is possible a MGB exists then a MGB exists. Using only B, if it is possible a MGB exists it only follows that a MEB exists. I'll have to give this more thought.

PPS: I'm still confused. I'll have to give this more thought.

PPS: This is confusing. It's hard to think in a modality that does not assume transitivity. Transitivity is what tells us that if a proposition is necessarily true, then it is necessarily true that it is necessarily true. It is hard to think in a modality where something might be both necessarily true, and yet possibly not necessarily true. So at this point, working in B, I think if a MGB exists it does not follow it is necessarily true a MGB exists. If a MGB exists, it follows that there is a MEB that necessarily exists. But it does not follow in B that it is necessarily true that it is necessarily true that MEB exists. And so it does not follow it is necessarily true a MGB exists. Therefore, working in B, even if we grant that it is possible it is true a MGB exists, it does not follow it is possible it is necessarily true a MGB exists, and therefore it does not follow a MGB exists. It only follows that a MEB exists.