Algebraic Graph Theory: Distinct Eigenvalues and Sensitivity

Talk by Shahla Nasserasr.

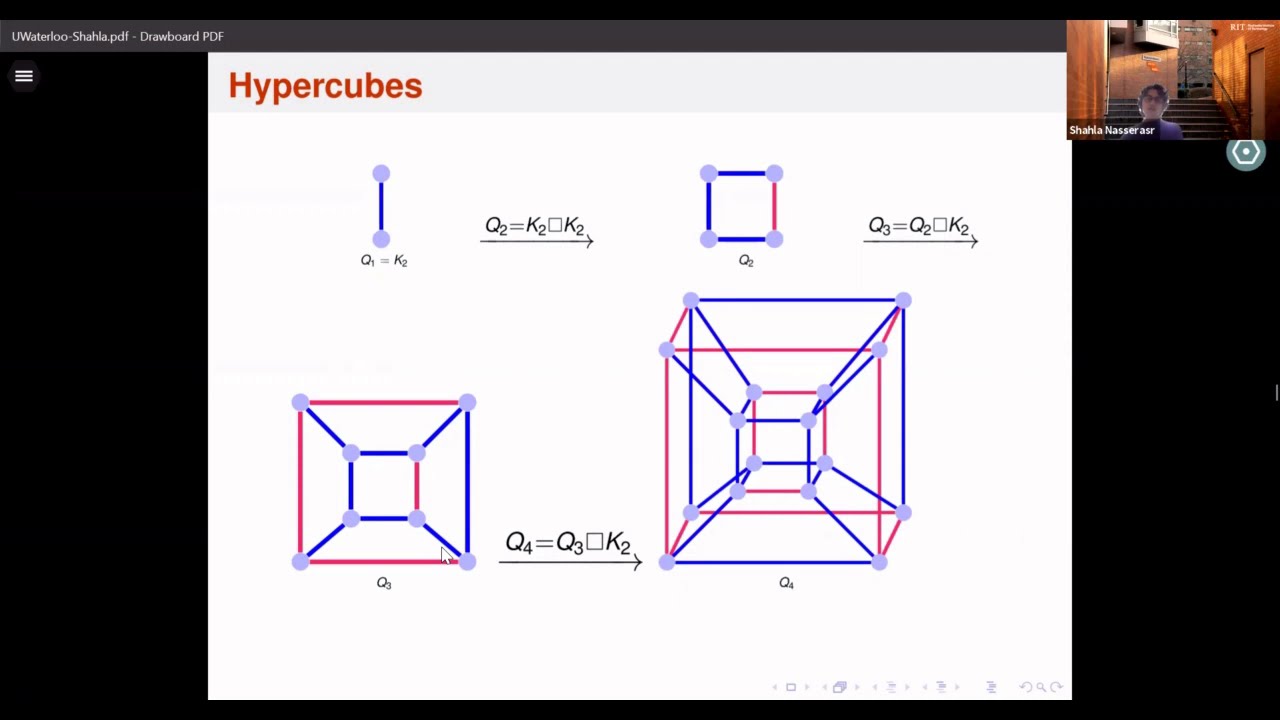
For a graph G, the class of real-valued symmetric matrices whose zero-nonzero pattern of off-diagonal entries is described by the adjacencies in G is denoted by S(G). The inverse eigenvalue problem for the multiplicities of the eigenvalues of G is to determine for which ordered list of positive integers m_1 ≥ m_2 ≥ ... ≥ m_k with summation as i goes from 1 to k of m_i equal to the number of vertices of G there exists a matrix in S(G) with distinct eigenvalues λ_1, λ_2, ... , λ_k such that λ_i has multiplicity m_i. A related parameter is q(G), the minimum number of distinct eigenvalues of a matrix in S(G). The main focus of this talk will be on the parameter q(G). A relationship between some of the techniques that are used in studying graphs with q(G)=2 and in solving the sensitivity conjecture will be presented. This is joint work with the Discrete Mathematics Research Group of Regina.