Oct 14, 2022: Ambat Vijayakumar (Split graphs with four distinct eigenvalues)

Title: Split graphs with four distinct eigenvalues
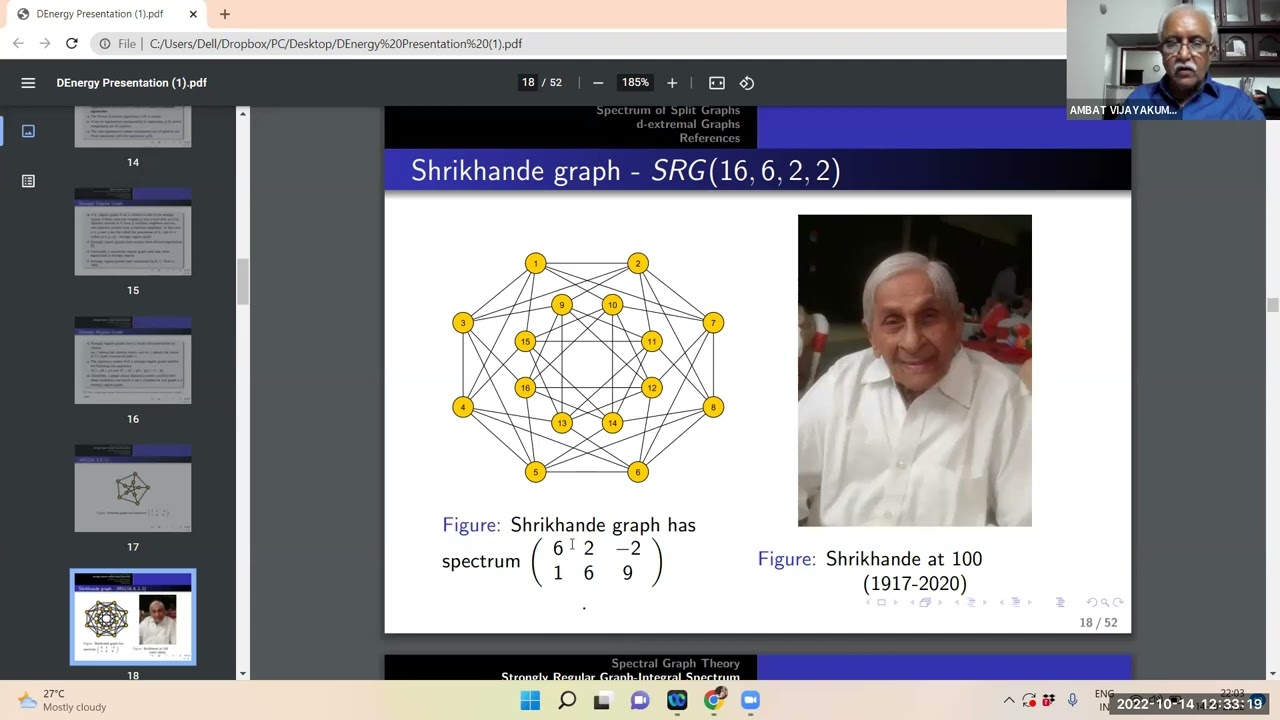
Abstract: The adjacency matrix of a connected graph G is an n × n matrix A(G) = [aij], where aij = 1 if the vertices vi and vj are adjacent and aij = 0 otherwise. The spectrum of G is {λ1, ... , λn}, where λ i 's are the eigenvalues of A(G). The adjacency matrix and eigenvalues of a connected graph have been studied intensively in literature. It is a well-known fact that a graph of diameter d has at least d+ 1 eigenvalues. Let us call a graph d-extremal if it has diameter d and exactly d + 1 eigenvalues. Such graphs have been intensively studied by various authors. A graph is split if its vertex set can be partitioned into a clique and a stable set. Such a graph has diameter at most 3. We obtain a complete classification of the connected bidegreed 3-extremal split graphs. We also show how to construct certain families of non-bidegreed 3-extremal split graphs. This is a joint work with Felix Goldberg, Steve Kirkland and Anu Varghese.