filmov
tv
Saddle points

Показать описание
Just because the tangent plane to a multivariable function is flat, it doesn't mean that point is a local minimum or a local maximum. There is a third possibility, new to multivariable calculus, called a "saddle point".
Saddle points
Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3
Calc 3 Ch.14 Find Local Maxima | Local Minima | Saddle points of the Function | Example #1
Use the Second Derivative Test to Find Any Extrema and Saddle Points: f(x,y) = -4x^2 + 8y^2 - 3
Multi-variable Optimization & the Second Derivative Test
Local Max, Min and Saddle Points - Full Example Explained
Local extrema and saddle points of a multivariable function (KristaKingMath)
Game theory [Operations research]- Part 2- Saddle point- 10 solved examples
Extreme Values | Absolute and Relative Maxima & Minima | Critical Point | Saddle Point | SYBSc K...
19. Saddle Points Continued, Maxmin Principle
Local Extrema and Saddle Points of f(x,y) Example 2
Extreme Values and Saddle Points | Explained with Several Examples
How to Find Saddle Point in a game theory? Topic :-Operation Research
2x2 Systems of ODEs: Saddle Points and Instability
Ex 2: Classify Critical Points as Extrema or Saddle Points - Function of Two Variables
How To Bend A 3 Point Saddle EMT Conduit.
Calc III: Find local max, min and saddle point of a surface
Local extreme Values | Maxima & Minima | Saddle Point | Critical Point | Numericals | Maths 1
Calc III: Finding local max/min, saddle points
Calc 3 Ch.14 Find Local Maxima | Local Minima | Saddle points of the Function | Example #2
Ex 1: Classify Critical Points as Extrema or Saddle Points - Function of Two Variables
Spotlight Talk: How to Escape Saddle Points Efficiently
14.7.1 Local Extrema & Saddle Point
Saddle Point Of A Matrix
Комментарии
 0:05:50
0:05:50
 0:14:35
0:14:35
 0:05:49
0:05:49
 0:05:20
0:05:20
 0:13:36
0:13:36
 0:04:45
0:04:45
 0:11:23
0:11:23
 0:10:54
0:10:54
 1:11:42
1:11:42
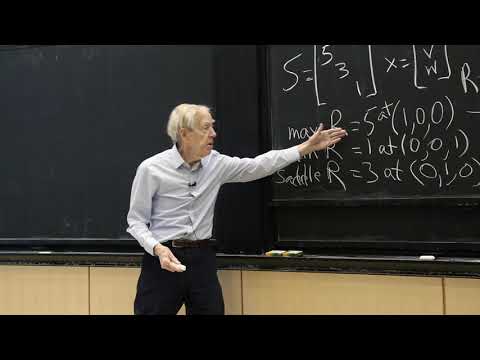 0:52:13
0:52:13
 0:14:24
0:14:24
 0:24:05
0:24:05
 0:05:17
0:05:17
 0:27:43
0:27:43
 0:10:05
0:10:05
 0:01:30
0:01:30
 0:10:27
0:10:27
 0:22:52
0:22:52
 0:07:00
0:07:00
 0:03:18
0:03:18
 0:06:15
0:06:15
 0:16:19
0:16:19
 0:13:07
0:13:07
 0:09:01
0:09:01