filmov
tv
Find a+b+c+d

Показать описание
This problem is from the Harvard-MIT Mathematics Tournament. It was a good way to ease myself back to making videos after a break.
Find a+b+c+d
If A:B, B:C, C:D, D:E are given,then Find A:B:C, A:B:C:D and A:B:C:D:E
Solve Ratio a:b:c:D in just 1 second #viralmaths #navneetsir #adda247
Find the value of a, b, c and d from the equation:
Find a, b, c, d given Critical Point Information in cubic function
Ratio and Proportion - Amazing Shortcut Trick Find A:B:C and A:B:C:D easily - Competitive Exams
Find the values of a,b,c and d from the equation [ a-b 2a+c 2a-b 3c+d ] = [ -1 5 0 13 ]|NCERT|CBSE
If 4A=5B=6C, then find A:B:C ? @Y5Teaching
Classification of Fires | Type A,B,C,D,E,K
Find a,b,c Given Vertex is (1,4) And Passes through (-1,-8). Quadratic Function
`a+b+c=6'and'1/a+1/b+1/c=3/2` , then find `a/b+b/c+b/a+b/c+c/a+c/b`
BCD addition Example
43/30=a+1/(b+1/(c+1/d) a+b+c+d=? a,b,c,d natural numbers. How to solve this quickly and logically?
Find the value of a,b,c and d which satisfy matrix
If 6A= 4B= 9C; find A:B:C(#SSCCGL Maths Questions)
If a:(b+c) =1:3 and c:(a + b) =5:7 then find (b: a+c)
A/3=B/4=C/7 then find (A+B+C)/C=?
If A:B = 4:5 and B:C = 7:8, then find A:C ?
If A:B = 2:3 B:C = 5:4 C:D = 3:7 then find the value of A:B:C:D
find pressure at A, B, C, and D | hydrostatic pressure| sample problem
a/b+c = 2/3 , b/a+c = 5/7 find a::b:c | ratio most important questions
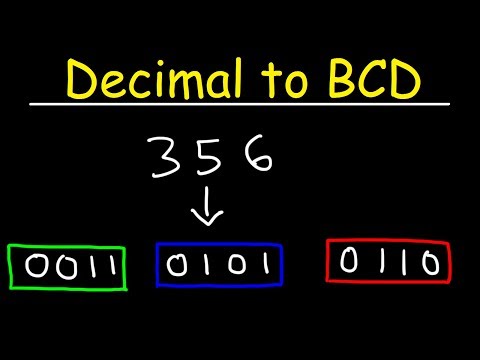
Decimal to BCD
If A:B = 5:6 and B:C = 4:7, find A:B:C
Find A:D | If A:B=2:3, B:C=4:5 and C:D=6:7, let us find A: D | Ratio & Proportion solution | AA
Комментарии
 0:11:13
0:11:13
 0:06:12
0:06:12
 0:00:31
0:00:31
 0:04:34
0:04:34
 0:03:21
0:03:21
 0:06:35
0:06:35
 0:02:13
0:02:13
 0:00:55
0:00:55
 0:05:15
0:05:15
 0:03:40
0:03:40
 0:02:27
0:02:27
 0:06:24
0:06:24
 0:04:14
0:04:14
 0:06:00
0:06:00
 0:01:55
0:01:55
 0:03:27
0:03:27
 0:00:40
0:00:40
 0:00:54
0:00:54
 0:04:08
0:04:08
 0:10:03
0:10:03
 0:04:36
0:04:36
 0:05:38
0:05:38
 0:04:06
0:04:06
 0:03:16
0:03:16