filmov
tv
Complex Conjugation and Cubic Polynomials with One Real Root (Algebra 3: Lecture 27 Video 2)

Показать описание
Lecture 27: We started this lecture by discussing Galois groups of cubic polynomials f(x) in F[x] where F is a field of characteristic not equal to 2 or 3. When f(x) is reducible things are straightforward, and when f(x) is irreducible the Galois group is either isomorphic to S3 or to A3 depending on whether the discriminant of f(x) is a square in F. We saw that if K/Q is a Galois extension (where we think of K as a subfield of C), then complex conjugation restricts to an element of Gal(K/Q). We used this to see that if f(x) is an irreducible polynomial in Q[x] with exactly one real root, then Gal(f) is isomorphic to S3. We discussed a generalization to the case of irreducible degree p polynomials with exactly p-2 real roots where p is a prime. We then adapted the ideas from our discussion of cubic polynomials to give a procedure to determine the Galois group of a quartic. A key idea was to consider the resolvent cubic of the quartic. At the end of the lecture we discussed some problems involving the Galois group of quartics of the form x^4+ax+b.
Reading: In this lecture we closely followed Section 14.6, pages 611-615. We also discussed several Algebra Qualifying Exam problems: Fall 2010 #5, Spring 2013 #5a, Fall 2001 #4, Fall 2014 #5, and Fall 2019 #7. At the very end of lecture we mentioned Exercises 13 and 14 in Section 14.6 of the textbook.
Reading: In this lecture we closely followed Section 14.6, pages 611-615. We also discussed several Algebra Qualifying Exam problems: Fall 2010 #5, Spring 2013 #5a, Fall 2001 #4, Fall 2014 #5, and Fall 2019 #7. At the very end of lecture we mentioned Exercises 13 and 14 in Section 14.6 of the textbook.
 0:11:19
0:11:19
 0:16:53
0:16:53
 0:08:05
0:08:05
 0:04:54
0:04:54
 0:05:54
0:05:54
 0:05:06
0:05:06
 0:03:10
0:03:10
 0:15:02
0:15:02
 0:00:37
0:00:37
 0:03:22
0:03:22
 0:17:47
0:17:47
 0:05:39
0:05:39
 0:01:00
0:01:00
 0:04:17
0:04:17
 0:04:49
0:04:49
 0:03:17
0:03:17
 0:07:39
0:07:39
 0:07:13
0:07:13
 0:05:07
0:05:07
 0:09:27
0:09:27
 0:12:22
0:12:22
 0:02:04
0:02:04
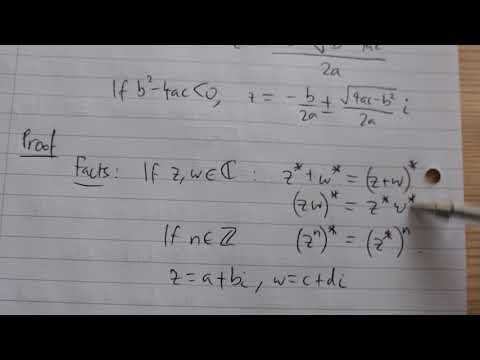 0:07:27
0:07:27
 0:07:07
0:07:07