Relations and Functions: The Modern Definition of a Mathematical Function.

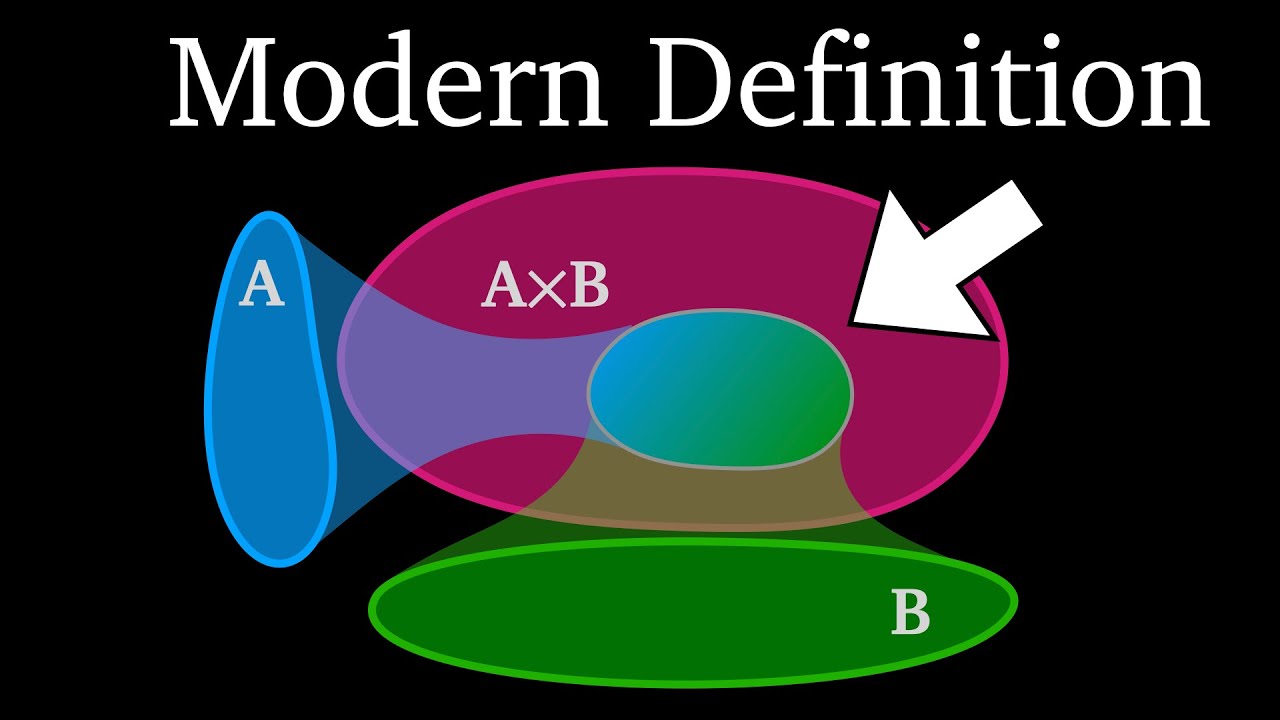
In this video, we discuss how the definition of a function has changed over time, largely due to the development of set theory.

Chapters
0:00 - Introduction and Motivation
01:50 - Products of Sets
02:53 - Relations
03:59 - Functions

The product links below are Amazon affiliate links. If you buy certain products on Amazon soon after clicking them, I may receive a commission. The price is the same for you, but it does help to support the channel :-)

In-video references

FAQ : How do you make these animations?
Animations are made in Apple Keynote which has lots of functionality for animating shapes, lines, curves and text (as well as really good LaTeX). Editing and voiceover work in DaVinci Resolve.

Supporting the Channel.
If you would like to support me in making free mathematics tutorials then you can make a small donation over at
Thank you so much, I hope you find the content useful.

[DrWillWood]

I didn't go into too much detail in the video but the reason this definition came about is because there was a phase in the 19th/early 20th century when mathematicians (notably, David Hilbert) wanted to establish every object/thing in mathematics in it's most basic or foundational form. Hence, here we have the definition of a function made entirely from sets and set theory!

[curtiswfranks]

I feel like this video deserves a follow-up concerning injectivity, surjectivity, and bijectivity. :)

[keithphw]

Interesting, thanks! For others wondering, the square wave is function then, even though it appears to have vertical sections with more than y per x, based on Wikipedia which defines its domain to exclude the integers at the vertical sections.

[hououinkyouma]

I misread it as what is fuction of mathematics.

And now I know what function are in mathematics.

❤

[richardlopez]

Thank you so much. The first video I watch that explains what is a function with its pure meaning inside set theory.

[boium.]

A friend of mine came up with some new notation based on a programming language I forgot the name of.

He introduced 4 symbols, but this notation can be expanded.

Let A and B be sets. We call f a general mapping if it is just any subset of AxB. We will denote this by f: A * -> * B.

A fuction is a subset of AxB were for all x in A, there exist a y in B such that (x, y) is in the subset, and for any x in A, if (x, y) and (x, z) is in the subset, then y=z. This is to say that if we look at all the elements in the subset. We will find every element of A once and only once, while any element of B may appear anywhere between 0 to infinity many times. We will denote this by f: A !->* B

Sometimes we do a little bit of notational abuse and are not able to map every element from the domain to the output space. (Example, we write f: R -> R, for f(x) = 1/x, while we should write f: R/{0} -> R). If we look at the subset of AxB that discribes such a "function", we'll notice that we are missing some x in A such that (x, y) is in the subset for some y. We either see any elementen once, or not at all. We denote this by f: A ?->* B and called it a partial function.

Last example before I start explaining. We call f: A !->+ B a surjection.

So what do all these symbols mean? well, they indicate how many times an element of A (or B respectively) show up at part of an element in the subset of AxB that discribes the mapping.

!: 1
?: 0 or 1
*: 0 to ∞
+: 1 to ∞

With this notation, we exactly know how the mappings behave, and this can be expanded to include more symboly. Also, the behaviour of inverses of mappings are quite easy to determine. Example, we call f a injection if it is f: A !->? B. The inverse of this is simplily f^-1: B ?->! A. We see that it sort of behaves like a partial function, exept that any valid input has only one output. We called any mapping of this form an inverse injection.

I could go on with all the names for the 16 different types of maps you get with this notation, but this is already a long text. Try to see what mappings/functions have which behaviour for yourself.

Edit: third paragraph, youtube makes stars dissaprear when I type them too close to eachother, so I put extra spaces in the notation of a general mapping.

[Woollzable]

Great video as usual! Keep up the good work!

[APDesignFXP]

This is amazing and a great refresher before my winter terms!

[lumipakkanen]

As a tangent you could've mentioned some issues with this definition compared to the naive rules-based (constructive) approach: Take A to be the set of even natural numbers greater than 2 and B to be the set of primes. Define the relation to be that y of B is the smallest prime of all prime pairs that make up a given x of A. There is currently no quaranteed way to produce such y and it's not even known if a requisite prime pair exists to begin with (Goldbach's conjecture). Assuming the conjecture this relation still defines a function. Contrast this with a rules-based approach that always produces an answer in a straightforward way.

[SwordQuake]

But what about injection, surjection and bijection?

[marcrg]

For another video talk about the definition of the cartesian product as a set, such as Kuratowski's:
AxB={{{x}, {x, y}} for x in A, y in B}
Its pretty amazing how things that seem to be "primitive ideas" in fact are not that foundational :)

[devinwilliams]

There are, however, such things are multi-valued functions. I encountered this when doing complex analysis in my undergraduate, though we didn't dwell on it long enough, it was just for defining the logarithm function on the entire complex plane, so I don't know much about them if it goes any further than that and if the idea of a function goes even further than that, would be interested in seeing that.

[guilhemescudero]

Love the video! Clear as Crystal! Furthermore, love the black background :)
I do have a question, given the definition of a function you give there, does the square wave you introduced at 0:37 is a function ?
Here my note well formed arguments :
· for all (x, y) | x \in R, y \in R and for all (v, w)| v in R, w \in R, v≠x, y=w, YES (existence and unicity of the ordered paire) which describes paires of the "horizontal lines"
· for all (x, y) | x in R, y in R and for all (v, w)| v in R, w in R, v=x, y≠w, NO (existence and ¬unicity of the ordered paire) which describes paires of the "vertical lines"

So the overall answer for me is no according to this argument

Thank you for what you do :)

[the_allucinator]

The function f: A->B being a subset of set AxB reminds me of Curry-Howard Isomorphism... like how exponents is related to multiplication.

Any possible combination of input (A) and output (B) may constitute a function.

[o_-_o]

I would have mentioned
Riemann surface

[Anujkumar-mywi]

This definition of function seems to differentiate from the usual 'process' conception of function that we have .

[dacianbonta]

not a solution. just obfuscated the difficulties under set theory fog.

[TheArtikae]

Meanwhile programmers:
Look at my function. It takes no parameters and returns no value.

[Lemon_Inspector]

Today I will add "codomain of a function" to the list of maths concept that give me nightmares, though this one seems more like David Hilbert's fault rather than God's.

[ivarorno]

I reject rule 2, there are plenty of multi-valued functions, why are people so hung up on single-valued functions?