Google Interview Riddle - 3 Friends Bike and Walk || Logic and Math Puzzle

Google interview puzzle :
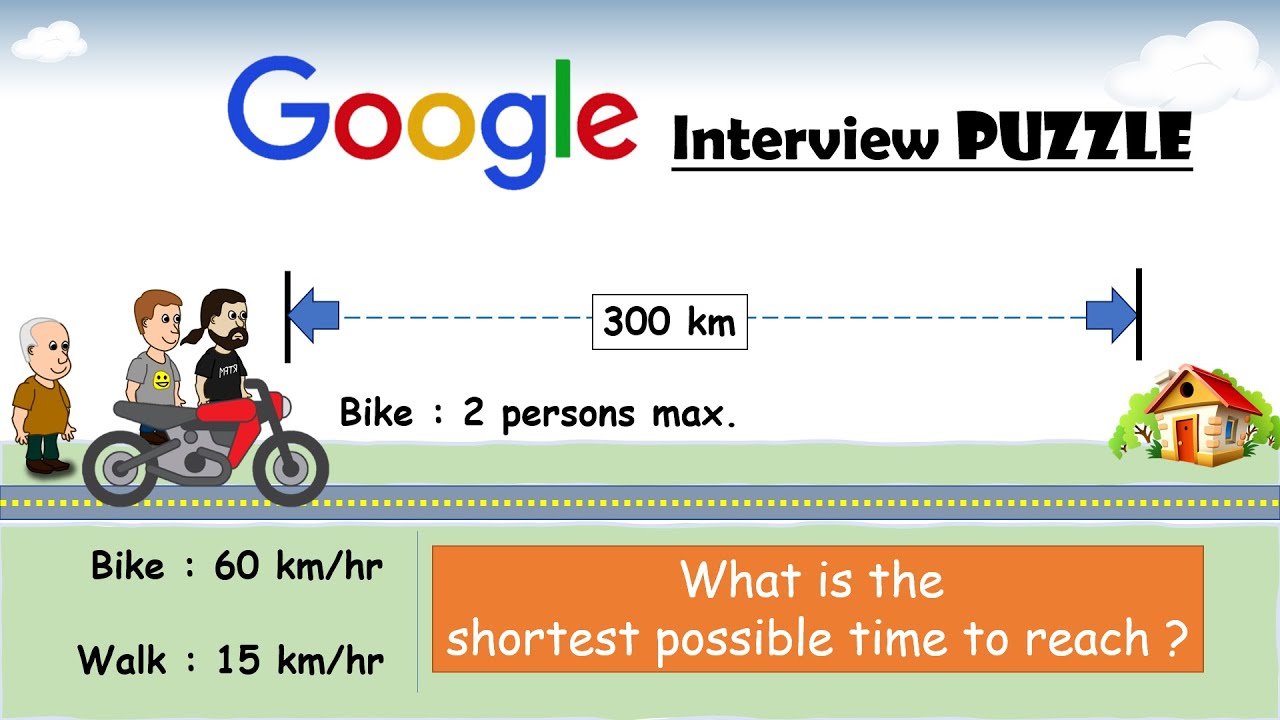
Three brothers Alex, Bob and Carl travel to visit their uncle who lives exactly 300 kms away from their house, to celeberate his birthday.
They have a motorbike (bike) which can carry a maximum of two persons at a time.
Assume that the bike has a constant speed of 60 km/hr.
Each brother can walk at a speed of 15 km/hr.
The brothers are brilliant logicians, just like you.
If, they all start from their house at the same time.
what is the shortest possible time in which they all can reach their destination.
Pause the video and think logically.

It's an amazing Google interview riddle to challenge your intelligence.
So if you are looking for a job at Google, please study optimization based puzzles in detail.

You can share puzzles and riddles with me on these links:

Also try these brilliant mind blowing puzzles:

5 Pirates PUZZLE (Version 2) | 100 Gold Coins 5 Pirates

Trains & Bird Puzzle || Challenge for Math and Aptitude lovers

Very Tricky Race Puzzle

[angirasnazar]

In India, it doesn't matter what the capacity of a bike is, people adjust themselves anyhow 😂😂😂

[MysticIndie]

Bob is going to win Gold medal in next Olympics by walking 86 km at 15 km/hr. 🥇

[utsavkumarvats]

The one riding bike never walked 😂😂he Is real genius

[FoodFFacts]

Everyone : Calculate how many hours
Me : who the hell able to walk 15km/hr

[saurabhkondkar]

this is how i carry my two friends on a bike while in blue zone in pubg...

[jensraab]

I took a slightly modified approach that of course yields the same results but is, I think, less confusing as it requires only one unknown and is perhaps a little more intuitive.

The basic idea is very similar to the one of the video: the "biking brother" carries one of the "walking brothers" some distance, drops him off, and returns to the point which the other "walking brother" has reached, picks him up and drives again towards the uncle's house where all of them arrive simultaneously.
The "trick" is to realize that the first walking brother walks a distance x before he's carried the remaining way to the uncle, while the second walker is first carried on motorbike and then walks the rest - but since they must both spend the same time walking and going on motorbike respectively in order to arrive at the uncle's house, the distance where the second walker is dropped off is the same distance x that the first walker goes before being picked up.

So, for both walkers the following equation is true:
t = x / v₁ + (s-x) / v₂; x being the unknown partial distance, s being the total distance (i.e. the 300 km), and v₁ and v₂ the velocities of the walking and riding the motorbike respectively
I habitually approach problems with the general case and plug in the specific numbers later. The downside, I know, is that plugging in the numbers first might speed up the solution but the upside is that one gets a solution that is valid for *all* cases - different numbers? --> you just plug in different values at the very end! ;-)

Back to the problem. Let's now focus on the lucky bastard who doesn't have to walk at all.
He will first cover the total distance s minus the partial distance x where he drops off the first brother. When he goes back, the other brother's already walked partial distance x and the go the remainder all the way to the uncle, i.e. also (s - x).
What about the bit when he's going the other way after having dropped of the first brother to pick up the second? This is the total distance s with the partial distance x missing on both ends, i.e. (s-2x).
In total, the biker goes (s-x)+(s-2x)+(s-x) = (3s-4x).
Going with motorbike speed, he'll need the following time for this:
t = (3s-4x) / v₂

These two expressions must be equivalent and therefore:
x / v₁ + (s-x) / v₂ = (3s-4x) / v₂

We perform, I quote, "simple calculation" and plug in the numbers to learn that x is 600/7 km and t is 9 ²/₇ h.

OK, that last line was a bit facetious. It is easier to plug in the numbers first but if one continues with the general case one finds that the partial distance x is:
x = 2sv₁ / (v₂ + 3v₁)
and the time to reach the uncle's house is:
t = s/v₂ * [3 - 8 / (v₂/v₁ + 3)]
Like I said above, the beauty of these general solutions is that they will work for any value of the given parameters.

[ashutoshsharma]

Uncle :- Why you guys are late?
3 Fellows :- Actually we are wasting time in equating a way to reach in less time.

Edit :- I think I have a good humour that I make 1k+ people laugh.

[shahriarhussain]

Legends say:
They never reached their uncle's house as they are still trying to solve the complex equation.
😂

[sivapradeep]

Ultra optimised solution:
Call their uncle to the brothers house
Then it would take only 5hrs😂😂😂

[rocketfrog]

I did it this way in my head:

Once I figured out that to maximize efficiency, all 3 brothers needed to arrive at the same time, and that meant the "walking" brothers each had to walk (and ride) the same distance, I called the walking distance "X". The dropoff point is X from the destination, and when the biker returns to the pickup point, it will be X from the origin. The distance in between the pickup and dropoff is "Y".

The entire distance can be split in three sections: X -> Y -> X

Now the question is: how far is X and Y? To figure it out, we can compare how far the brothers go in the same time period; from the start until the original walker is picked up by the rider.
One brother walks distance X to the pickup in the time that the biker goes X+Y to the dropoff, then Y again back to the pickup, or X+2Y.
We know that riding is 4x as fast as walking (60km/h) / (15km/h), so if the walker went X, he would have gone 4X, had he been riding.
We know that the distance the rider went, and the distance the walker would have went if he were riding, are equal
Therefore the equation is X+2Y=4X
reduce to Y=1.5X

The distance from origin to destination can now be rewritten as a ratio: 1:1.5:1 (from X:Y:X)
To use integers for ease, double it to 2:3:2
This splits the total distance into sevenths, X is 2/7 of the total distance, and Y is 3/7 of the total distance

So the "walking" brothers walk 2/7 of the way and ride 5/7 of the way
The rider rides 5/7 of the way (X+Y), drops off his brother, rides back 3/7 of the way (Y), picks up the other brother, and rides 5/7 of the way to the origin, for a total of:
5/7 + 3/7 + 5/7 = 13/7
The rider rode 13/7 of the total distance, which was 300km, or 300*13/7=557 & 1/7km
557 1/7km @ 60km/h = 9 2/7 hours

No complex equations or calculations required. I'm curious, how easy was it to follow my solution?

[JonathanSpencer]

***Alternative solution***
We know optimal solution involves a drop off and a pick up. Let x, y, and z be time to first drop off, time between drop off and pick up, and time until finish.
Eqn1: 15(x+y) + 60z = 300 (distance of initial walker)
Eqn2: 60x + 15(y+z) = 300 (distance of initial passenger)
Eqn3: 60(x - y + z) = 300 (distance traveled by motorcycle, has to backtrack so y is negative)

3 equations, 3 unknowns, no problem.
Eqn1 + Eqn2 + 2*Eqn3 -> x + z = 50/7
Sub that solution back into Eqn3 and find y = 15/7
Total time elapsed
x + y + z = 65/7 = 9.28

[Rahul_Hindu_Mondal_]

Meanwhile in *INDIA* :

ALEX SITTING ON TANKER OF BIKE
BOB DRIVING
CARL SITTING IN BACK

[riankardison]

Bob doesn't wasting time. He would be cleaning their uncle's house while waiting for the other 2. Their uncle would gives bob some money to buy fuel for their motorcycle. Everyone is happy now

If they are brothers in their teens, they will fight for who will go on bike first and end up all three walking dragging their bike along.

[md.afzalbari]

First i get the ans - 11 hrs and then i know the correct approach to solve this. Thanks man👍

[jgoemat]

I took the easy route. I figured out what would happen if Alex dropped Bob off at the 300km mark in 5 hours and let him keep walking. Carl moved 75km and is 225km from the 300km mark. As Alex moves back to pick up Carl they will be moving towards each other at 75km/h and will meet in 3 hours at the 120km mark, and Bob moved another 45km so he's at 345km. Now Alex and Carl have to catch up to Bob at 45 km/h relative speed and he is 225 km away so that's another 5 hours. They all end up at the 420km mark in 13 hours so no matter the distance using this arrangement their average speed will be 420/13 km/h. 420km/300km is 7/5, so they could get to 300km in (13*5)/7 hours, or ~9.29 hours

[Victor-evvu]

What if uncle isn't at home😂.They all will waste time

[random]

“Simple calculation”

Maybe when I was in year 10.

As an engineer 20 years on. No chance

[AdilAmanullah]

Imagine the calculations goes wrong and Bob arrives a month later

[vladschiopu]

So we basically have 3 walking Usain Bolts that never get tired, and they have a weird motorcycle that reach 60km/h instantly, but can't go faster