filmov
tv
Mathe RÄTSEL Geometrie – Wie lang ist x?

Показать описание
Rätsel Geometrie
In diesem Mathe Lernvideo erkläre ich (Susanne) wie man die Aufgabe mit dem Satz des Pythagoras und einem Gleichungssystem lösen kann. Mathematik einfach erklärt.
0:00 Einleitung – Mathe Rätsel
1:03 Lösung
3:11 Satz des Pythagoras
4:45 Gleichungssystem lösen
9:22 Bis zum nächsten Video :)
Jetzt Kanalmitglied werden und meinen Kanal unterstützen:
MEIN KOMPLETTES EQUIPMENT
Unterstütze mich gerne mit ein paar Münzen für eine Tasse Tee! 🍵
ÜBER MICH
📱 Mein Insta: @mathema_trick
Adresse für geschäftliche Anfragen und Fanpost:
Susanne Scherer
Gaustraße 8, F32
67655 Kaiserslautern
Päckchen und Pakete bitte direkt an die DHL Packstation senden:
Susanne Scherer
1054501450
Packstation 179
67655 Kaiserslautern
#Radius #Mathe #MathemaTrick
In diesem Mathe Lernvideo erkläre ich (Susanne) wie man die Aufgabe mit dem Satz des Pythagoras und einem Gleichungssystem lösen kann. Mathematik einfach erklärt.
0:00 Einleitung – Mathe Rätsel
1:03 Lösung
3:11 Satz des Pythagoras
4:45 Gleichungssystem lösen
9:22 Bis zum nächsten Video :)
Jetzt Kanalmitglied werden und meinen Kanal unterstützen:
MEIN KOMPLETTES EQUIPMENT
Unterstütze mich gerne mit ein paar Münzen für eine Tasse Tee! 🍵
ÜBER MICH
📱 Mein Insta: @mathema_trick
Adresse für geschäftliche Anfragen und Fanpost:
Susanne Scherer
Gaustraße 8, F32
67655 Kaiserslautern
Päckchen und Pakete bitte direkt an die DHL Packstation senden:
Susanne Scherer
1054501450
Packstation 179
67655 Kaiserslautern
#Radius #Mathe #MathemaTrick
Mathe RÄTSEL Geometrie – Wie lang ist die Strecke?
Mathe RÄTSEL Geometrie – Wie lang ist x?
Kannst du diese Mathe-Rätsel lösen? | Mathe-Rätsel Test für Genies!
Die Leitungen dürfen sich nicht schneiden ☝️😰 #rätsel #matherätsel #geometrie #gehirnjogging #logik...
Mathe RÄTSEL Geometrie – Kannst du es lösen?
Mathe RÄTSEL Geometrie – Wie groß ist der Radius?
Ein schönes Geometrie Rätsel – Was kommt raus?
Mathe RÄTSEL Geometrie – Wie groß ist der Flächeninhalt?
Findest du eine Lösung? 🧐 #rätsel #rätselchallange #geometrie #mathe #gehirnjogging #iqtest
Mathe RÄTSEL Geometrie – Berechne den Umfang!
Mathe RÄTSEL Geometrie – Wie groß ist der Flächeninhalt?
Wie ist das möglich? 😳 #rätsel #matherätsel #geometrie #zeichnen #art #hack #mathetrick #mindblowing...
LANDESWETTBEWERB Mathematik – Rätsel Geometrie
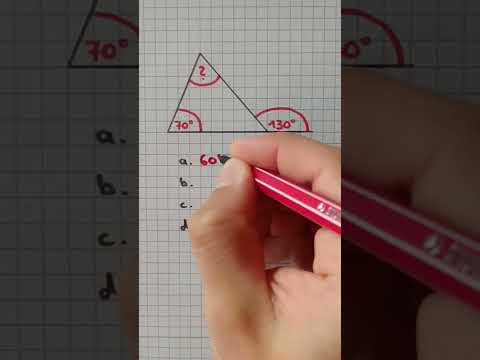
Wie groß ist der Winkel? 🤔 #geometrie #dreieck #test #matherätsel
⁉️⁉️ MATHE RÄTSEL GEOMETRIE | Wie groß ist das Quadrat?
Mathe RÄTSEL Geometrie – Schaffst du es?
Wer kann mir das erklären?! 😳 #rätsel #geometrie #matherätsel
Mathe RÄTSEL Geometrie – Dreieck
Mathe RÄTSEL Geometrie – Kannst du es lösen?
👀 Mathe Basics #162 👀 Berechne den Flächeninhalt des Kreises | Geometrie-Rätsel | ObachtMathe...
Weißt du die Antwort? ✍️ #geometrie #mathe #aufgabe #test #winkel
Das Leiterproblem | ohne Taschenrechner | Mathe Rätsel Geometrie
Mathe RÄTSEL Geometrie – Wie groß ist der Flächeninhalt der Kreisfigur?
Kannst du die rote Fläche berechnen? – Mathe Rätsel Geometrie
Комментарии
 0:08:23
0:08:23
 0:09:33
0:09:33
 0:00:12
0:00:12
 0:00:16
0:00:16
 0:09:51
0:09:51
 0:09:06
0:09:06
 0:09:58
0:09:58
 0:15:57
0:15:57
 0:00:12
0:00:12
 0:07:32
0:07:32
 0:09:29
0:09:29
 0:00:12
0:00:12
 0:14:11
0:14:11
 0:00:12
0:00:12
 0:03:39
0:03:39
 0:13:44
0:13:44
 0:00:11
0:00:11
 0:07:22
0:07:22
 0:06:50
0:06:50
 0:03:56
0:03:56
 0:00:12
0:00:12
 0:15:14
0:15:14
 0:09:43
0:09:43
 0:06:30
0:06:30