Ch7Pr26a: Kernel and Nullity of a 4x3 matrix

preview_player
Показать описание
How to find the kernel and nullity of a 4x3 linear transformation. This is Chapter 7 Problem 26a of the MATH1231/1241 Algebra Notes, presented by Norman Wildberger of UNSW.
  1. MathsStatsUNSW
  2. Mathematics
  3. UNSW
  4. Kernel
  5. Rank–nullity Theorem
  6. Matrix (Literature Subject)
Рекомендации по теме
Ch7Pr26a: Kernel and 0:09:58

Ch7Pr26a: Kernel and Nullity of a 4x3 matrix

Ch7Pr26b: Kernel and 0:04:55

Ch7Pr26b: Kernel and Nullity of a 3x4 matrix

Image and Kernel 0:05:35

Image and Kernel

1.6 Ex2 Finding 0:02:45

1.6 Ex2 Finding kernel and range

KERNEL and RANGE 0:08:46

KERNEL and RANGE of a LINEAR TRANSFORMATION - LINEAR ALGEBRA

Determine the Null 0:57:49

Determine the Null Space (Kernel) and Nullity of a Linear Transformation

The rank nullity 0:03:16

The rank nullity relation and examples

Given a linear 0:08:25

Given a linear transformation, find the kernel and range

Sec 4.8 Example 0:18:03

Sec 4.8 Example 1: Kernel, range, and rank-nullity for a linear transformation

The Kernel of 0:02:47

The Kernel of a Linear Map

Kernel and Image 0:10:34

Kernel and Image of a Linear Transformation | Linear Algebra | Griti

Kernel and Image 0:06:06

Kernel and Image of a Linear Transformation Example 1 | Linear Algebra | Griti

Rank and Nullity 0:03:30

Rank and Nullity of A Example 2

Determine a Basis 0:04:16

Determine a Basis for the Kernel of a Matrix Transformation (3 by 4)

Linear Algebra - 0:10:38

Linear Algebra - Lecture 32 - Dimension, Rank, and Nullity

kernel and range 0:00:08

kernel and range of a linear transformation and thier dimensions

Example of Kernel 0:06:31

Example of Kernel and Range of Linear Transformation

Rank Nullity Theorem 0:06:46

Rank Nullity Theorem | Linear Algebra | Griti

RANK and NULLITY 0:10:46

RANK and NULLITY of a Matrix | FREE Linear Algebra Course

Sec 4.8 Example 0:17:32

Sec 4.8 Example 2: Kernel, range, and rank-nullity

Tutorial Q39 -- 0:10:29

Tutorial Q39 -- rank and nullity relations of matrix

Week 9 - 0:01:57

Week 9 - Rank-nullity theorem

Rank and nullity 0:07:42

Rank and nullity of linear map, Rank and Nullity Theorem

Linear Algebra 3.3. 0:09:29

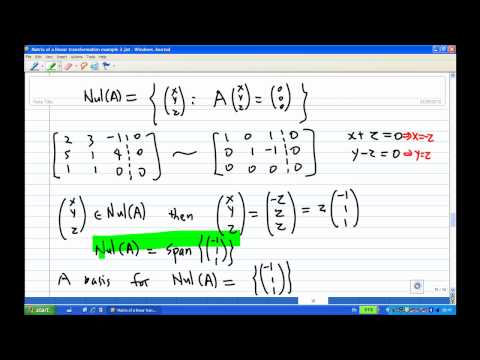
Linear Algebra 3.3. Nullity/Kernel of a Matrix A. Finding the basis.

Комментарии
Автор

Prof Wildberger you are a fantastic teacher. Praying Tanaka has a final very soon and was struggling with this topic, but your conceptual explanation and the example were really helpful. Praying Tanaka hopes to dig through your lectures and find one on orthogonality too- another topic that didn't really click.

nataliatothemoon
Автор

what's the name of the song in the beginning please. Quite delightful.

enyioma
Автор

he is really a teacher and his experiences speaks aloud

FreedomForKashmir
Автор

sir this is a 3x4 matrix. how do u determine the dimension is it based on the column or rows

hariharannair
Автор

So the reason the nullity/dimension of the kernal is ONE (and the subspace is a line) is the occurence of THREE pivot columns in RREF, leaving a SINGLE parameter.

abajabbajew
Автор

Thank you so much, this was so clear and informative!.

AbooddHamdan
Автор

Thankyou so much❤🎉well explained and clear understandable

micahteiul
Автор

Why is it R^4 at 0:50 ? The dimension of the environment isn't given by the lines of the matrix (which represent the coordinates of the vector)? The columns represent the no of vectors, not the coordinates which give the environment's dimension

psawyer
Автор

Thank you sir for the clear explanation.

dragonz_breath
Автор

you have a mistake on the 0's columns 0, 0, 1 is 0, 0, 0

jmzefren
Автор

Looks like it's -1/3 R2 for a new R2.

rcfoley