filmov
tv
A Radical Equation | Math Olympiads

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Radical Equations
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Solving A Radical Equation | Math Olympiads
Solving A Radical Equation #math #algebra #radicals
Solving A Radical Equation | Algebra
A Quick and Easy Radical Equation
Simplifying A Radical Expression
【ALGEBRA】 Math Olympiad | Radical Equation: can you solve it? | An exercise is included. | f141
A Golden Radical Equation
Radical equation – each step to solve…
A step-by-step guide on how to solve Radical Equation.
An Infinite Radical Expression
A radical equation.
Solving A Radical Equation | Algebra
Working with A Radical Expression
Solving A Radical Equation #algebra #radicals #radicalequations
What Is a Radical Expression in Math? : Radical Numbers
A Deep Dive into Nested Radical Equations #maths
Can You Solve a Radical Equation?
Evaluating A Radical Expression
Solving A Radical Equation | Algebra
Solving A Radical Equation | Algebra
Solving a Radical Equation
Комментарии
 0:17:11
0:17:11
 0:03:11
0:03:11
 0:18:05
0:18:05
 0:06:47
0:06:47
 0:00:46
0:00:46
 0:00:29
0:00:29
 0:09:16
0:09:16
 0:00:51
0:00:51
 0:00:55
0:00:55
 0:00:33
0:00:33
 0:14:34
0:14:34
 0:01:00
0:01:00
 0:00:40
0:00:40
 0:13:35
0:13:35
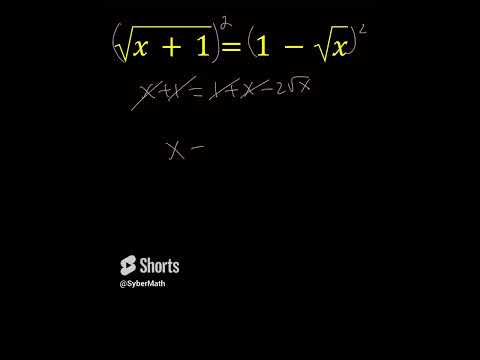 0:00:14
0:00:14
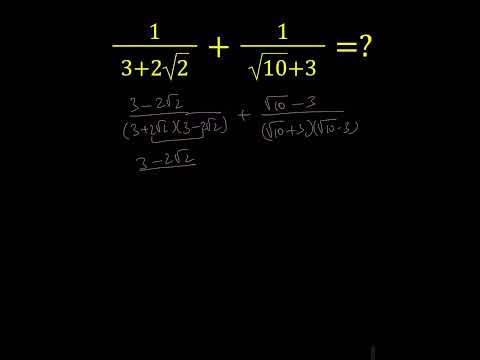 0:00:56
0:00:56
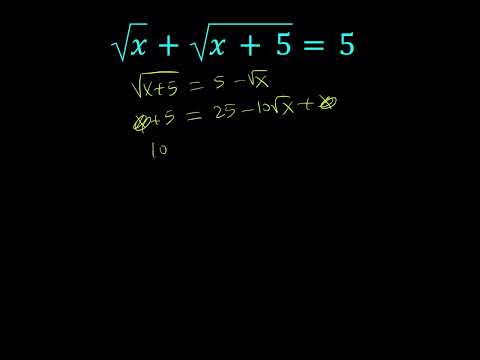 0:00:31
0:00:31
 0:02:36
0:02:36
 0:00:40
0:00:40
 0:00:31
0:00:31
 0:00:33
0:00:33
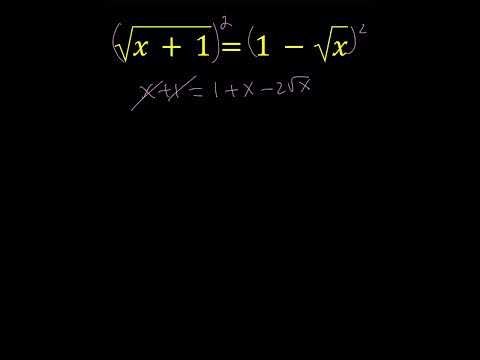 0:00:14
0:00:14
 0:00:38
0:00:38
 0:01:00
0:01:00