filmov
tv
derivative of (1+1/x)^x
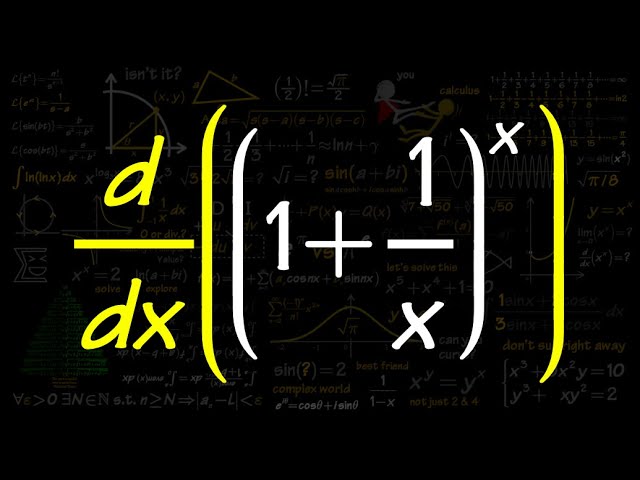
Показать описание
More derivative examples:
blackpenredpen
blackpenredpen
derivative of (1+1/x)^x
Shortcut For Derivative of x^x
derivative of 1/x using the power rule, derivative of 1/x
Derivative of 1/x with Power Rule | Calculus 1 Exercises
Derivative of 1 / x || A truly Geometric Proof without Infinitesimals
How to Find the Derivative of 1/x from First Principles
Derivative of 1/1+x || 1/(1+x) Derivative
derivative of x^(1/x), calculus 1 tutorial
NDA 1 2025 Exam Maths Live - Applications of Derivatives - Class 4
how do we know the derivative of ln(x) is 1/x (the definition & implicit differentiation)
Derivative of y = (x-1)/(x+1)
Proof: the derivative of ln(x) is 1/x | Advanced derivatives | AP Calculus AB | Khan Academy
Visual derivative of x squared
Proof: Derivative of ln(x) = 1/x by First Principles
MASTER Derivatives In Less Than A Minute!!
derivative of ln(1+1/x), two ways
How to Find the Derivative of 1/sqrt(x) using the Definition of the Derivative
What is the Derivative of 1 by root x || 1/root(x) Derivative
Derivative of (x + 1)/(x - 1) from First Principle | Class 11 Maths | JP Sir
x+1/x Tricks for competitive exams | Algebra Questions for SSC CGL NTPC Railway Exams
This is a very famous limit
Derivative of 1/x from First Principle | Class 11th Maths | JP Sir
Visual Derivative Definition!
derivative of ln(1/x) vs derivative of 1/ln(x)
Комментарии
 0:08:03
0:08:03
 0:00:52
0:00:52
 0:00:34
0:00:34
 0:01:32
0:01:32
 0:06:29
0:06:29
 0:02:53
0:02:53
 0:01:44
0:01:44
 0:09:51
0:09:51
 1:09:37
1:09:37
 0:16:49
0:16:49
 0:00:55
0:00:55
 0:08:08
0:08:08
 0:00:58
0:00:58
 0:08:14
0:08:14
 0:00:58
0:00:58
 0:03:58
0:03:58
 0:07:42
0:07:42
 0:01:30
0:01:30
 0:05:06
0:05:06
 0:00:24
0:00:24
 0:00:48
0:00:48
 0:03:08
0:03:08
 0:01:00
0:01:00
 0:02:45
0:02:45