filmov
tv
sin(n) does not converge - the subsequence approach

Показать описание
We look at the limit, as n tends to infinity, of sin(n), where n are integers.
00:00 Intro
00:07 Continuous limit
01:41 Discrete limit - idea of the proof
03:18 Proof that sin(n) does not converge
00:00 Intro
00:07 Continuous limit
01:41 Discrete limit - idea of the proof
03:18 Proof that sin(n) does not converge
The Sequence a_n = sin(n)/n Converges or Diverges Two Solutions with Proof
Proof that sum(sin(n)/n) Converges using Dirichlet's Test
checking for absolute convergence, series of sin(2n)/(1+2^n), calculus 2 tutorial
Series sin(1/n) diverges
sum of sin n/n^2 converges or diverges?
(Squeeze Thrm) Limit n goes to Infinity (sin(n))/n
Converging and Diverging Sequences Using Limits - Practice Problems
Does Infinite Series SUM((1 + sin(n))/10^n) Converge or Diverge?
How to Prove the Squence a_n = sin(n)/sqrt(n) Converges using the Squeeze Theorem
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Determine if series converges or diverges. {sin(1/n)}. Limit Comparison Test with harmonic series
Sum (-1)^n*sin(1/n) convergence. No sin(1/n) convergence, but passes sine alternating series test.
using complex numbers to evaluate the sum of sin(n)/n
incredible sin sin sum
Does Sum(sin^3(1/n)) Converge or Diverge?
Prove That the Limit sin x does not exist as x approached infinity by Heine Definition AP Calculus
the sum of sin(n)/n by using the Fourier Series (fourier series engineering mathematics)
sin(n) is dense!
Ex: Determine if a Sequence in the Form (sin(an))/n^b+c) is Bounded, Monotonic,and Convergent
Series Convergence and Divergence Using The nth Term Test sum(n*sin(1/n))
sin(nx) goes to 0
sin(314159...)
Reduction Formula for Integral of ∫sin^n(x)dx
Sinn Tegiment Scratch Resistant Test
Комментарии
 0:02:47
0:02:47
 0:10:56
0:10:56
 0:05:36
0:05:36
 0:05:33
0:05:33
 0:05:05
0:05:05
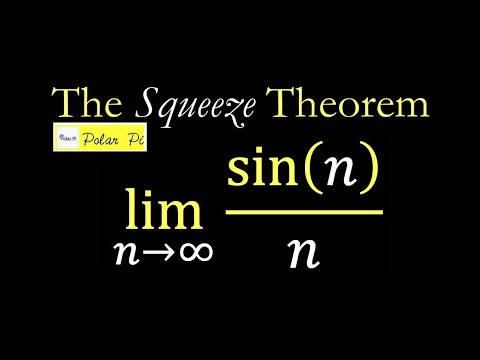 0:02:08
0:02:08
 0:30:13
0:30:13
 0:05:06
0:05:06
 0:02:28
0:02:28
 0:05:36
0:05:36
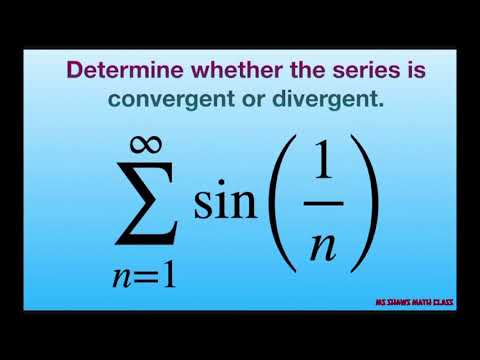 0:04:07
0:04:07
 0:04:51
0:04:51
 0:11:31
0:11:31
 0:02:49
0:02:49
 0:04:17
0:04:17
 0:06:59
0:06:59
 0:08:27
0:08:27
 0:16:19
0:16:19
 0:06:48
0:06:48
 0:02:03
0:02:03
 0:21:50
0:21:50
 0:17:16
0:17:16
 0:07:40
0:07:40
 0:05:17
0:05:17