Area and volume | Wild Linear Algebra A 4 | NJ Wildberger

Area and volume in Linear Algebra are central concepts that underpin the entire subject, and lead naturally to the rich theory of determinants, a key subject of 18th and 19th century mathematics.

This is the fourth lecture of a first course on Linear Algebra, given by N J Wildberger.

Here we start with a pictorial treatment of area, then move to an algebraic formulation using bi-vectors. These are two-dimensional versions of vectors introduced in the 1840's by Grassmann.

The three dimensional case of volume uses tri-vectors.

Video Contents:
0:00 Intro
0:07 Overview
1:05 Area of Fundamental Figures
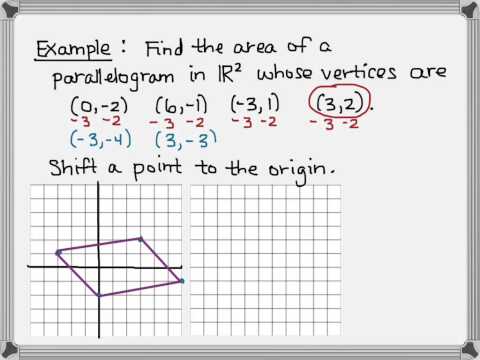
2:03 Area of a Parallelogram
6:34 Generalizing to an Arbitrary Parallelogram
11:52 Bi-Vectors
15:10 Physical Examples of Bi-Vectors 1
21:12 Physical Examples of Bi-Vectors 2
25:51 Physical Examples of Bi-Vectors 3
28:41 Bi-Vectors in the Plane 1
30:58 Bi-Vectors in the Plane 2
34:03 Unit Bi-Vectors and Area
39:27 Using Bi-Vectors to Compute Area
42:43 Invariance of Ratios of Areas in Affine Geometry
45:51 Three Dimensional Affine Space
49:05 Using Tri-Vectors to Compute Volume
53:23 Exercises

************************

Here are the Insights into Mathematics Playlists:

Here are the Wild Egg Maths Playlists (some available only to Members!)

************************

[DAToft]

Why haven't I found this channel before... I've found a gold mine!

[lidorshimoni]

exterior algebra. from lecture to lecture I love you more and more.

[JhunnyAshRose]

Nice explanation! it helped me a lot, thank you professor!

[gn]

Interesting lecture, but that's not how you use a crescent wrench (should turn ccw from the opposite side to loosen).

[sacul]

Video contents

0:00 Intro
0:07 Overview
1:05 Area of Fundamental Figures
2:03 Area of a Parallelogram
6:34 Generalizing to an Arbitrary Parallelogram
11:52 Bi-Vectors
15:10 Physical Examples of Bi-Vectors 1
21:12 Physical Examples of Bi-Vectors 2
25:51 Physical Examples of Bi-Vectors 3
28:41 Bi-Vectors in the Plane 1
30:58 Bi-Vectors in the Plane 2
34:03 Unit Bi-Vectors and Area
39:27 Using Bi-Vectors to Compute Area
42:43 Invariance of Ratios of Areas in Affine Geometry
45:51 Three Dimensional Affine Space
49:05 Using Tri-Vectors to Compute Volume
53:23 Exercises

[jigawatt]

It seems like this calculation of area only works if the affine coordinate system has basis vectors that are perpendicular. This, for example, is most pronounced in the External Method of area calculation at around 3:50, where the outer parallelogram's area is calculated first. A parallelogram, whose adjacent sides are not perpendicular, cannot have its area calculated by simply multiplying 2 adjacent sides together, as is done here; area in that case must be base * perpendicular height. While area that way would be guaranteed if the coordinate system had perpendicular basis vectors, it does not seem to work in the general affine coordinate system, which has no concept of perpendicularity. Please explain, then, how the determinant generalizes to finding area in any affine coordinate system. Thank you for the excellent lectures!