WildLinAlg4: Area and volume

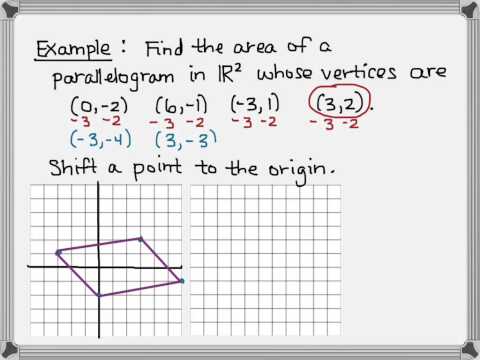
This video introduces the Linear Algebra approach to area, and to volume. It also introduces bi-vectors, with applications from physics: torque, angular momentum and motion in a magnetic field.

NJ Wildberger is also the developer of Rational Trigonometry: a new and better way of learning and using trigonometry---see his WildTrig YouTube series under user `njwildberger'. There you can also find his series on Algebraic Topology, History of Mathematics and Universal Hyperbolic Geometry.

[unswelearning]

Hi Kurtlane

That is correct. You can perform as many transpositions as you like--each changes the sign by -1.

[LakeWijaya]

Thans for the lectures!, good job. But there is an error, i think, on page 12. g1 and g2 are 'wedged' in the wrong order. As stated both bivectors have an area of 14 (in stead of 14 and -14)

[DannyWrigley]

Is it a mistake to think of these concepts as a generalization of cartesian algebra/geometry? It seems like this renders all the math usually taught before linear algebra into a special case of these ideas- namely one where a right angle bivector determines the plane by which you measure all quantities within it.

Thanks for all these videos, I appreciate the time you put into them, and that you care to share your knowledge with those who want to know as well. God bless!

[DannyWrigley]

Also, is your use of e as a symbol for the reference vector of a given plane a convention that's related to the use of e in group theory as the identity element of a group? Thanks again.

[Kurtlane]

Are you saying that unlike vector, which can be characterized by a length and an angle, a bivector is two vectors at any angle to each other or the outside, as long as the two vectors change their length correspondingly, so that ad-bc stays the same. If so, what is the need for a bivector? We can just use ad-bc instead.

[Kurtlane]

In other words, if two bivectors have the same ad-bc (but not the same a, b, c, and d), are they just two different bivectors with the same ad-bc, or are they the same bivector?

Thanks.

[hugstablebear]

p13 In rule 3, you state "whenever we interchange any
two of them we agree that we get a minus sign".
Though true in 3D, this is only true in general when
you exchange neighboring vectors, because the rule
arises out a combination of the Associative Law and
that (pvq)=-(qvp):
=--(bvc)va=---(cvb)va, i.e. avbvc-->-cvbva is really
the result of 3 interchanges (-)(-)(-)=(-).
This view is needed in higher dimensions,
e.g. avbvcvd<> -dvbvcva.
p12 g1vg2=+14