Solving cos(sinx)=1/2

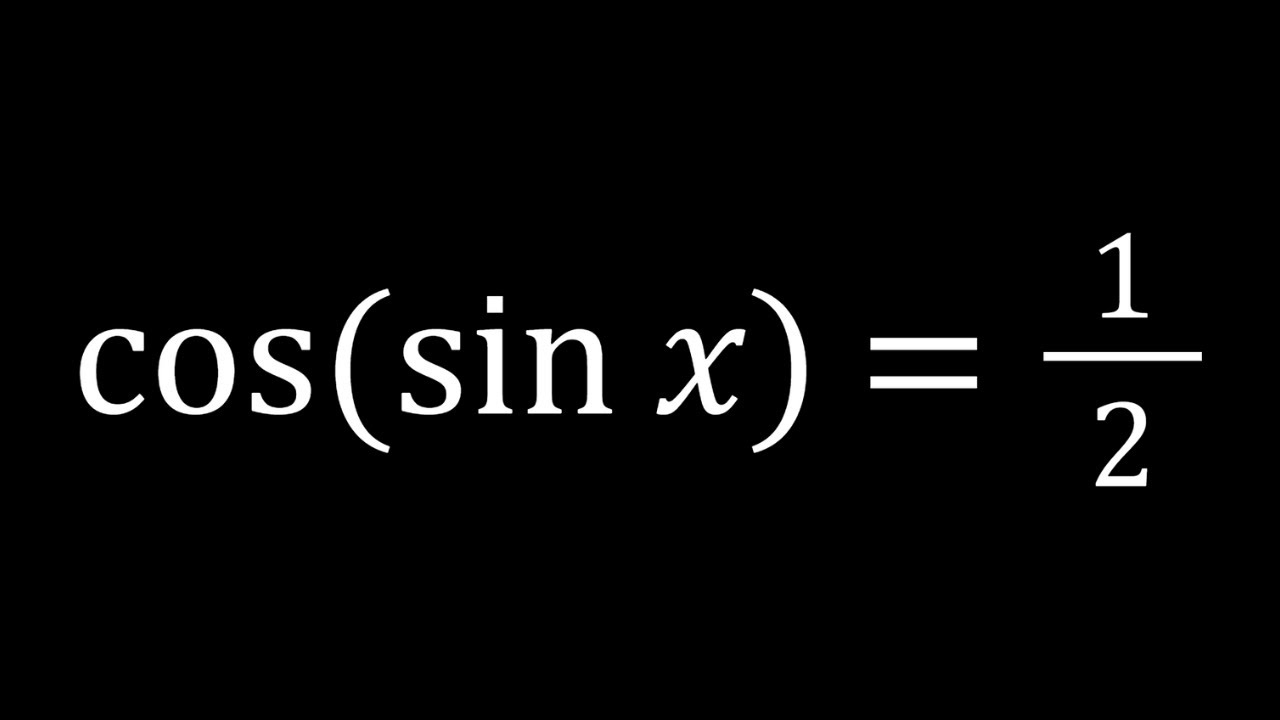
Показать описание

🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡

If you need to post a picture of your solution or idea:
#TrigonometryProblems #TrigonometricEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :

SyberMath

Рекомендации по теме

Комментарии

Syber’s been ignoring the complex solutions lately.💔

GreenMeansGOF

From ChatGPT:

There is no complex number z such that sin(z) = pi/3 exactly, because the sine function takes only real values for real arguments. However, we can find complex numbers whose sine is close to pi/3 by solving the equation numerically.

One way to do this is to use the definition of the sine function in terms of the exponential function:

sin(z) = (e^(iz) - e^(-iz)) / (2i)

Setting this equal to pi/3 and rearranging, we get:

e^(iz) - e^(-iz) = (2i) * pi/3

Multiplying both sides by e^(iz), we get:

e^(2iz) - 1 = (2i) * pi/3 * e^(iz)

Substituting y = e^(iz), we get a quadratic equation in y:

y^2 - (2i) * pi/3 * y - 1 = 0

Solving this quadratic equation using the quadratic formula, we get:

y = [(2i) * pi/3 ± sqrt((2i * pi/3)^2 + 4)] / 2

Simplifying and evaluating the square root, we get:

y = (i * pi/3) ± sqrt(1 - (pi/3)^2)

Taking the natural logarithm of both sides and solving for z, we get:

z = -i ln[(i * pi/3) ± sqrt(1 - (pi/3)^2)]

Therefore, the complex solutions for sin(z) = pi/3 are:

z = -i ln[(i * pi/3) + sqrt(1 - (pi/3)^2)] and z = -i ln[(i * pi/3) - sqrt(1 - (pi/3)^2)]

MichaelJamesActually

Awesome video . Nowadays I am waiting for your videos 😃❤

ashok_kumar

It's a TRIGONOMETRIC equation, not an exponential equation.

billtruttschel

What if x is complex? Are there any solutions then?

Blaqjaqshellaq

*sigh* x is gonna be complex, isn't it? pi/3>1

seroujghazarian

It should be plus minus pi/3 + 2i*pi*k where k is an integer, since cos is an odd function

cameronspalding

Hmm I guess there could be complex solutions, but by strict use of sin, the angles with cos=1/2 are pi/3, 2pi/3 etc. and -4pi/3 =5pi/3 etc. But even the closest of these to the range -1 to 1 are out of range. So there are no real solutions i think.

Qermaq

Actually there is no solution in the REAL world....
There are infinite solutions in the complex plain.

georget

No real solutions pi/3 is greater than 1

moeberry

ton équation revient à dire que sinx = pi/3 + 2kpi ou sinx = - pi/3 + 2kpi mais pi/3 est > 1 et - pi/3 < -1
donc ton équation ne comporte pas de solution réelle

jeanlismonde

sin x must be π/3 > 1 then there is no real answer.

yoshinaokobayashi

Solving cos(sinx)=1/2

Solving cos(sinx)=1/2

When sin x + cos x = 1/2, find the value of sin x cos x.

Solve the Trig equation sin x + cos x = 1 over the interval [0, 2pi)

Trigonometry Problems with Solutions | Sin x+Cos x=1/sqrt(2)

Interesting Trigonometry Problem | cos(sinx)=1/2

sin x cos x = 1/2, find value of x

Solve cos(x) - sin(x) = 1

Solve equation sqrt(3) sin x + cos x =1. Give general solution.

MATHS LAGERAHO || TRIGONOMETRIC FUNCTIONS COS(X+Y) = COS(X)COS(Y) - SIN(X)SIN(Y) || 6 MARKS || PU 1

sin(x)+cos(x)=sqrt(2) | Trigonometry

Using the sine function to find the missing length of the hypotenuse

Ex: Solve sin(x)=a Using a Calculator (positive a)

Solve cos x = -1/2

Решите уравнение ➜ sin⁡x+cos⁡x=1 ➜ 2 способа решения

Solve the Trig equation sin x - sqrt(3) cos x = 1 on the interval [0, 2pi)

Solve the Trig equation sqrt(3) sin x + cos x = 1 on the interval [0, 2pi)

How To Solve Trigonometric Equations With Multiple Angles - Trigonometry

sin(x) + cos(x) = 1 by Identities (Flawed)

Solve the Trigonometric Equation cos^2(x) - sin^2(x) = 1

Trigonometry For Beginners!

Solve the Trigonometric Equation sin(x)cos(x) = 1/4 by using Identities

équations trigonométriques simples - résoudre cos(x)=sin(x) & 2cos²(x)-1=0 - Première Terminale ...

Integral of sin(x)/(1+cos(x))^2 (substitution)

Find the solutions to a trig equation between 0 and 2pi