What is General Relativity? Lesson 36: Introduction to the Einstein Equation

What is General Relativity? Lesson 36: Introduction to the Einstein Equation

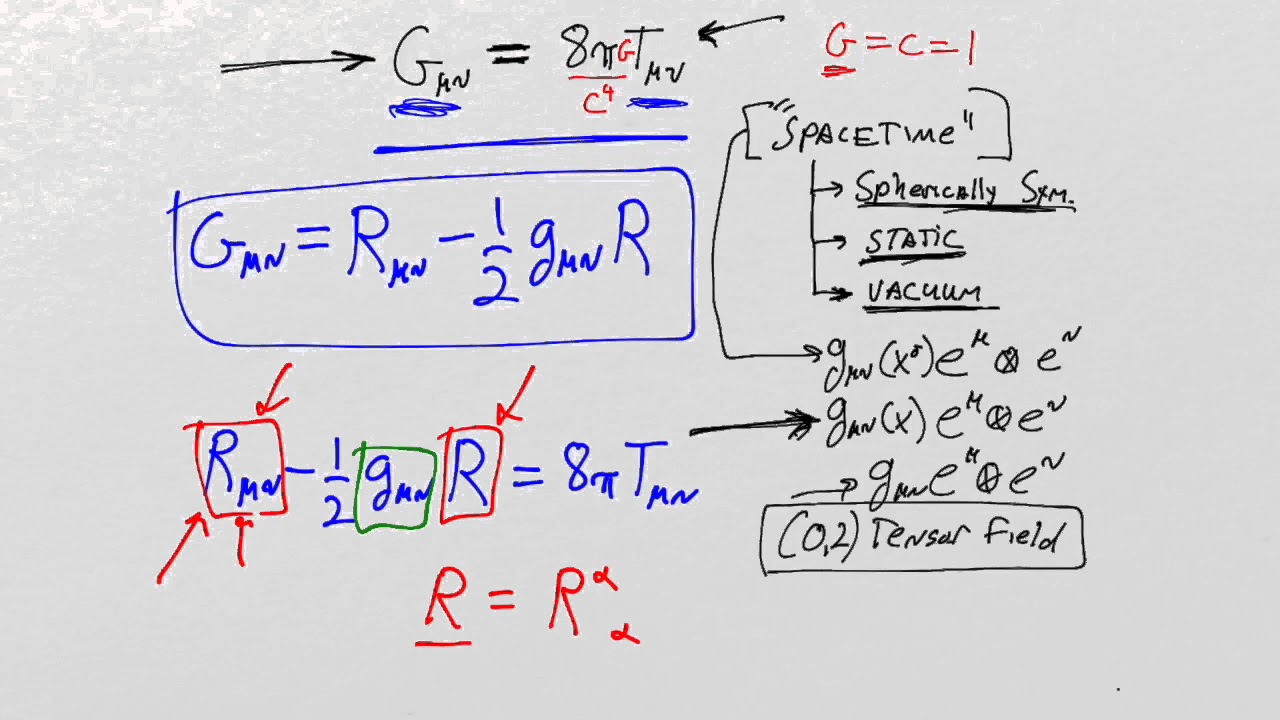
This lesson sets the stage for our attack on the Einstein equation.
NOTE and ERATA:
At 11:26 I called the Ricci Tensor the "Riemann Curvature Tensor" by mistake! R_ab is the "Ricci tensor"!

The paper by Kostic I occasionally refer to during these lectures can be found here:

I invite you to download the Catalog of Spacetimes at :

to use as a reference for the rest of the course.

Please consider supporting this channel via Patreon:

and discussing the material on the forums:

[sofarrell]

Thanks for this wonderful series of lectures.
One question - which # lesson do you pick up the topic of elliptic integrals again following on from lesson # 35?

[brianf]

Are there more Einstein equation lectures to come? I'm very interested in the topic and you are a great teacher.

[adriangheorghe]

Always write the tensors in Einstein's field equation, but never write the physical dimensions, in LMT or m Kg, s, of the terms in the equation. If the terms in the equation do not have physical dimensions and are only mathematical abstractions, I cannot figure out if the equation is physical and reflects real physical phenomena or if it is just a metaphysical equation, unrelated to physical reality. So please write me the physical dimensions of the terms in the relativistic equation of gravity.

[ericsu]

The angular difference between the perihelion and the aphelion on Einstein's geodesic is only 2 radians instead of 6.28 from the observation.
Click on "80. Schwarzschild's Geodesic and the Orbit of Mercury" on this website.

[harrycraig]

Thus whom is to judge you intellect by true facts?